Concentrations des solutions

Pour mettre en réaction de très faibles quantités de réactifs, il est souvent pratique d'utiliser des solutions de ces réactifs. Ces solutions sont, le plus souvent, des solutions aqueuses, mais peuvent être faites avec d'autres solvants si le composé est insoluble dans l'eau.
Il est également utile de connaître la quantité de composé dissout dans une masse ou un volume donné de solution, c'est-à-dire la concentration de cette dernière. Le but de ce chapitre est d'appréhender les outils nécessaires à:

comparer des solutions contenant des quantités différentes du même soluté.

modifier la concentration d'une solution (la diminuer, essentiellement).

En ce qui concerne les applications en lien avec ce chapitre, l'analyse de sang en est un exemple très concret. Notez que le sang est une solution aqueuse contenant plusieurs solutés, comme la bilirubine. Cette dernière est un "pigment jaune produit par la dégradation de l’hémoglobine des globules rouges. Le foie assure normalement son élimination. En cas de dysfonctionnement hépatique, la bilirubine s’accumule dans le sang et provoque un ictère (jaunisse)"¹.

Voilà le résultat des analyses de sang de deux individus pour la bilirubine:

adulte ($5\,\mathrm{L}$ volume total de sang), taux total de bilirubine $=\,55\,\mathrm{mg}$
enfant ($3\,\mathrm{L}$ volume total de sang), taux total de bilirubine $=\,36\,\mathrm{mg}$

Peut-on directement comparer ces deux valeurs? Si ce n'est pas le cas, comment les rendre comparables?

Résultat d'une prise de sang

Comment peut-on exprimer une concentration? Que se passe-t-il si on ajoute du solvant?

On ajoute du solvant, mais on aimerait que la concentration ne change pas. Que faut-il faire?

Encore un exemple. On trouve souvent dans la vie courante la notion de concentration : sur l’étiquette d’une bouteille sont indiquées les concentrations des sels minéraux, par exemple.

Prenons le cas de ces deux bouteilles de l'image ci-dessous:

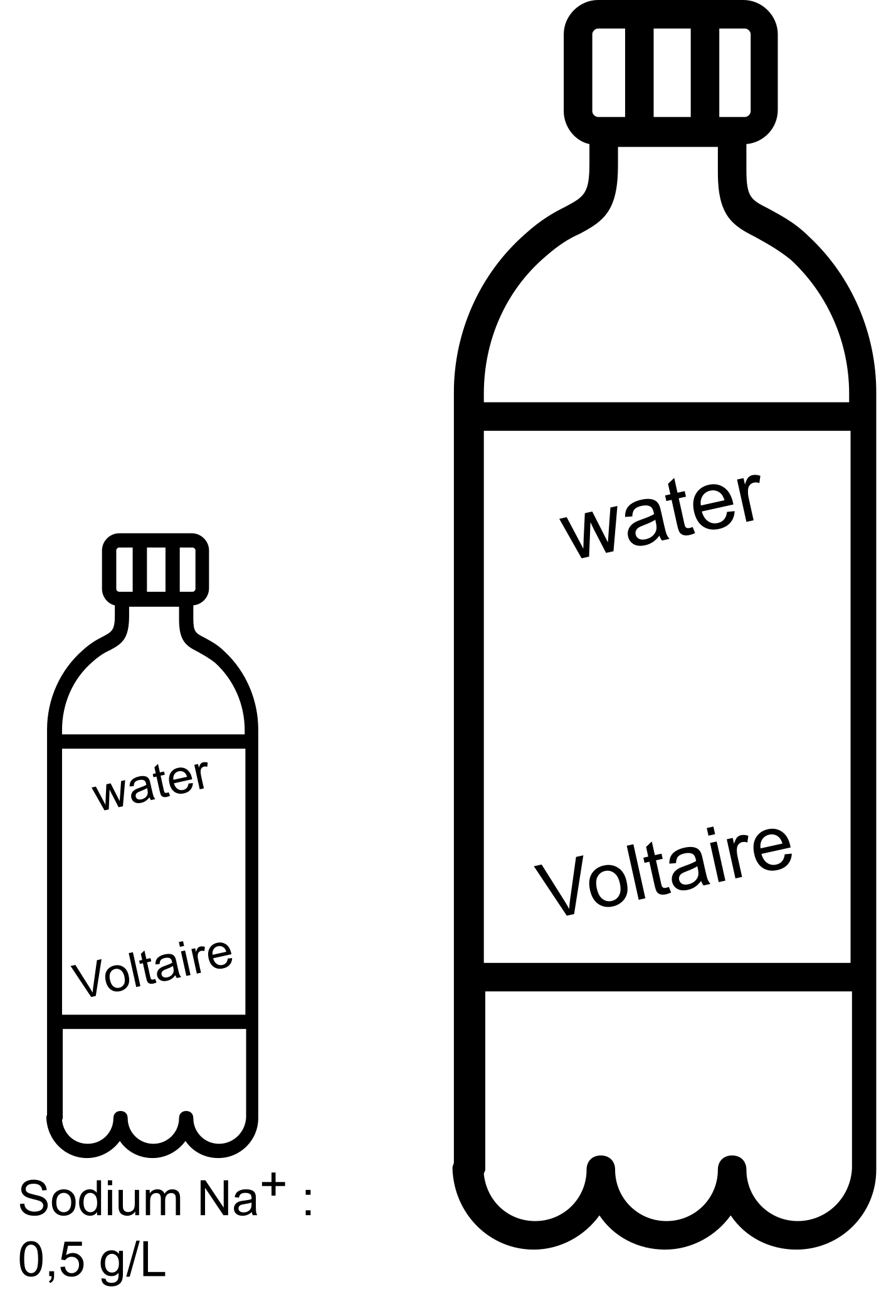
Sous quelle forme se trouve le sodium dans l'eau?

La concentration de sodium varie-t-elle si on prend un volume plus grand?

Que dire de la quantité de sodium?

L'icône de l'image ci-dessus a été modifiée à partir de Made by Made sur www.flaticon.com publiée sous license CC 3.0 BY

Expressions de la concentration d'une solution

Titre d'une solution ($\mathrm{g/mL}$ ou $\mathrm{g/L}$) :

Il indique la masse de soluté, en grammes, dans $1\,\mathrm{mL}$ ou $1\,\mathrm{L}$ de solution.
Une solution contenant $12\,\mathrm{g}$ de $\ce{NaCl}$ dans $100\,\mathrm{mL}$ a un titre ($t$) de :

Molarité ($\mathrm{mol/L}$) :

Il est très fréquent d'utiliser le nombre de moles de soluté dans un litre de solution. On nomme Molarité en composé $X$, le nombre de moles du composé $X$ dans un litre de solution.
Quelle est la molarité d'une solution contenant $4\,\mathrm{g}$ par litre de $\ce{NaOH}$ ($M$ = $40\,\mathrm{g/mol}$)?

Définitions

Concentration	Définition	Unité de mesure
Titre	masse en gramme de soluté contenu dans $1\,\mathrm{mL}$ ou $1\,\mathrm{L}$ de solution	$\mathrm{g/mL}$ ou $\mathrm{g/L}$
Molarité	nombre de mole de soluté contenu dans $1\,\mathrm{L}$ de solution	$\mathrm{mol/L}$

Calcul de la molarité à partir du titre

Pour une solution donnée, la molarité ($\mathrm{mol/L}$) et le titre ($\mathrm{g/L}$) sont proportionnelles.
La relation permettant de déterminer la molarité connaissant le titre est : $$ molarité=\frac{titre}{masse\,molaire}\Rightarrow \mathrm{\frac{\frac{g}{L}}{\frac{g}{mol}}=\frac{g}{L}\cdot \frac{mol}{g}=\frac{mol}{L}} $$

Et l'inverse (de la molarité au titre):

$$ titre=molarité\cdot masse\,molaire\Rightarrow \mathrm{\frac{mol}{L}\cdot \frac{g}{mol}=\frac{g}{L}} $$

Calculer la molarité d'une solution de $\ce{NaCl}$ dont le titre est $1,17\,\mathrm{g/L}$.

Calculer le titre (g/l) d'une solution de $\ce{NaOH}$ $0,25\,\mathrm{mol/L}$.

Volumes différents de $1\,\mathrm{L}$

Que se passe-t-il si le volume de la solution n'est pas égal à $1\,\mathrm{L}$?
On doit d'abord se ramener à $1\,\mathrm{L}$ : c'est à dire diviser la quantité donnée ($\mathrm{g}$ ou $\mathrm{mol}$) par le volume donné en $\mathrm{L}$.

Calculer la molarité d'une solution de $\ce{H2S}$ contenant $0,68\,\mathrm{g}$ de $\ce{H2S}$ dans $100\,\mathrm{mL}$ de solution.

Calculer le titre d'une solution de $\ce{H2SO4}$ sachant qu'elle contient $0,2\,\mathrm{mol}$ de $\ce{H2SO4}$ dans $50\,\mathrm{mL}$ de solution.

Dilution des solutions par adjonction d'eau

Diluer = augmenter le volume du solvant = ajouter de l'eau.
Diluer signifie donc que la concentration diminue, comme dans l'image ci-dessous².

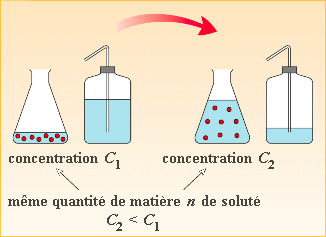
Une dilution comporte la diminution de la concentration. Notez que le nombre de moles de soluté ne varie pas. Après dilution, le soluté se trouve dispersé dans un volume plus grand.

Notez bien que lors d'une dilution, le nombre de moles du soluté ne varie pas: c'est la concentration à diminuer, car le soluté se trouve dans un volume plus grand de solvant.

Voici comment on peut procéder lors d'une dilution.

Comment préparer $500\,\mathrm{mL}$ de $\ce{NaOH}$ $0,5\,\mathrm{mol/L}$ à partir d'une solution de $\ce{NaOH}$ $2\,\mathrm{mol/L}$?

On identifie chaque donnée de l'énoncé:
- Molarité initiale=$M_i$=$2\,\mathrm{mol/L}$: c'est le molarité de la solution initiale, que l'on a à disposition.
- Molarité finale=$M_f$=$0,5\,\mathrm{mol/L}$: c'est la molarité de la solution à obtenir.
- Volume initial=$V_i$=$?$: c'est le volume de la solution initiale à prélever. Il est inconnu: on doit le calculer.
- Volume final=$V_f$=$0,5\,\mathrm{L}$: c'est le volume de solution à préparer.

Pour déterminer le $V_i$, on procède de la manière suivante:
on calcule d'abord les moles de soluté que l'on aura à la fin:

$$ mol_f=V_f \cdot M_f= 0,5\,\mathrm{L} \cdot 0,5 \mathrm{\frac{mol}{L}}=0,25\,\mathrm{mol} $$

Ce nombre de moles ne varie pas avec la dilution ($mol_i=mol_f$).
On peut ainsi déterminer le volume de la solution initiale $V_i$ qu'il faudra prélever.

$$ V_i=\frac{mol_i}{M_i}=\frac{0,25\,\mathrm{mol}}{2\,\mathrm{\frac{mol}{L}}}=0,25\,\mathrm{mol} \cdot \frac{1}{2}\,\mathrm{\frac{L}{mol}}=0,125\,\mathrm{L} $$

Il s'agit de prélever $125\,\mathrm{mL}$ d'une solution de $\ce{NaOH}$ de concentration égale à $2\,\mathrm{mol/L}$ qu'on transvase dans un ballon jaugé de $500\,\mathrm{mL}$ et on complète avec de l'eau jusqu'au trait de jauge.

On peut donc résumer, que, lors d'une dilution, le nombre de mole (=la quantité de composé dissout) ne change pas.
Nb initial de moles = Nb final de moles

$$ mol_i=mol_f $$

ce qui nous conduit à la formule finale:

$$ V_i \cdot M_i = V_f\cdot M_f $$

Exercices SERIE Concentration d’une solution A

Comment allez-vous procéder pour préparer au laboratoire :

$1\,\mathrm{L}$ de solution $1\,\mathrm{mol/L}$ de chlorure de sodium.

$1000\,\mathrm{mL}$ de solution $1\,\mathrm{mol/L}$ d'hydroxyde de sodium.

$100\,\mathrm{mL}$ de solution $0,1\,\mathrm{mol/L}$ de sulfate de cuivre ($II$).

Calculez la masse (en $g$) contenue dans :

$500\,\mathrm{mL}$ d'$\ce{H2SO4}$ $5\,\mathrm{mol/L}$

$25\,\mathrm{mL}$ de $\ce{Ca(OH)2}$ $10^{-2}\,\mathrm{mol/L}$

Calculez le nombre de moles de produits contenus dans :

$100\,\mathrm{mL}$ de $\ce{MgCl2}$ $0,5\,\mathrm{mol/L}$

$2\,\mathrm{L}$ de $\ce{H2SO4}$ $2\times 10^{-2}\,\mathrm{mol/L}$

$130\,\mathrm{mL}$ de $\ce{KOH}$ $2\times 10^{-2}\,\mathrm{mol/L}$

$5\,\mathrm{mL}$ d'$\ce{HNO3}$ $4\times 10^{-2}\,\mathrm{mol/L}$

Donnez la molarité en $\ce{H+}$ ou $\ce{OH-}$ de solutions contenant :

$6,8\,\mathrm{g}$ de $\ce{H2S}$ dans $100\,\mathrm{mL}$.

$18,75\,\mathrm{g}$ de $\ce{KCl}$ dans $2,5$ litres de solution.

$1,16\,\mathrm{mg}$ de $\ce{Ba(OH)2}$ dans $500\,\mathrm{mL}$.

$4,92\,\mathrm{g}$ de $\ce{H3PO3}$ dans $5\,\mathrm{mL}$ de solution.

Soit une solution $0,1\,\mathrm{mol/L}$ de $\ce{CaCl2}$.

Combien de moles d'ions $\ce{Ca^2+}$ et combien de $\mathrm{g/L}$ de $\ce{Ca^2+}$ contient-elle?

Combien de moles d'ions $\ce{Cl-}$ et combien de $\mathrm{g/L}$ de $\ce{Cl-}$ contient-elle?

Soit une solution de $4$ litres du mélange suivant : $3$ litres de $\ce{NaOH}$ $10^{-2}\,\mathrm{mol/L}$ et $1$ litre de$\ce{ NaCl}$ $0,2\,\mathrm{mol/L}$

Quelle masse de sodium y a-t-il dans ces $4$ litres?

Quelle est la molarité de $\ce{Na+}$ dans la solution finale?

Une solution de $\ce{Ca(OH)2}$ contient $0,025$ mole d'ions $\ce{OH-}$ par litre, quelle est sa molarité et quel est son titre ($\mathrm{g/mL}$)?

Combien de $\mathrm{mL}$ de $\ce{H2SO4}$ $10^{-2}\,\mathrm{mol/L}$ et combien de millilitres d'eau faut-il pour préparer $50\,\mathrm{mL}$ de $\ce{H2SO4}$ $5\times 10^{-3}\,\mathrm{mol/L}$?

Comment préparer $180\,\mathrm{ml}$ de $\ce{Na2SO4}$ $7,5\times 10^{-3}\,\mathrm{mol/L}$ à partir d'une solution de $\ce{Na2SO4}$ $1\,\mathrm{mol/L}$?

Comment préparer $100\,\mathrm{mL}$ de $\ce{HCl}$ $2,5\times 10^{-2}\,\mathrm{mol/L}$ à partir d'une solution $10^{-1}\,\mathrm{mol/L}$?

Un laborantin a à disposition une solution de sucre $2\,\mathrm{M}$. Un volume de $90\,\mathrm{mL}$ de cette solution est prélevé et ensuite versé dans un ballon jaugé de $250\,\mathrm{mL}$. Le laborantin complète avec de l’eau jusqu’au trait de jauge. Que vaut la molarité finale?

On dissout $15\,\mathrm{g}$ de sucre dans $150\,\mathrm{mL}$.

Que vaut le titre de cette solution?

On prélève $100\,\mathrm{mL}$ de la solution mère (=initiale), ci-dessus. Quelle est la quantité de sucre contenue dans les $100\,\mathrm{mL}$ prélevés?

Que vaut le titre si on ajoute $200\,\mathrm{mL}$ d’eau aux $100\,\mathrm{mL}$ prélevés?

L’acide sulfurique ($\ce{H2SO4}$) est une substance très corrosive qui a de nombreuses applications en chimie. On le retrouve dans les batteries des voitures, mais également de manière naturelle dans les pluies acides³. Nous disposons de $300\,\mathrm{mL}$ d’acide sulfurique $0,5\,\mathrm{M}$. Nous prélevons $25\,\mathrm{mL}$ de cette solution que nous mettons dans un ballon jaugé de $250\,\mathrm{mL}$ et que nous complétons, avec de l’eau, au trait de jauge.

Combien y a-t-il d’atomes de soufre dans la solution mère?

Quelle est la concentration molaire de la nouvelle solution?

Vous avez à disposition $2$ litres de jus obtenu en pressant $10$ citrons et en complétant avec de l’eau. À partir de cette solution, comment faut-il procéder pour obtenir $1$ litre de jus contenant $4$ citrons?
Détaillez la procédure avec du texte et des calculs.

Lorsqu’une solution de $\ce{Ba(OH)2}$ à $8,2\times 10^{-2}\,\mathrm{M}$ ($=\mathrm{mol/L}$) est mélangée à une solution de $\ce{Na2SO4}$ à $6,64\times 10^{-2}\,\mathrm{M}$, un précipité se forme. Combien de millilitres de chacune des deux solutions ont été nécessaires pour obtenir $9,45\,\mathrm{g}$ de ce précipité?

Soit l’équation suivante :
$\ce{Sn + 2 AgNO3 -> Sn(NO3)2 + 2 Ag}$
On veut oxyder $0,5\,\mathrm{g}$ d’étain métallique à l’aide d’une solution de nitrate d’argent de concentration $2\,\mathrm{M}$. Un volume de $10\,\mathrm{mL}$ de cette solution sera-t-il suffisant?

Soit l’équation:
$\ce{Na2CrO4 + SnCl2 + HCl -> CrCl3 + SnCl4 + H2O + NaCl}$

Equilibrez-la.

Pour réduire $10\,\mathrm{mL}$ de la solution d’oxydant, il faut $13,8\,\mathrm{mL}$ de la solution de réducteur
$0,05\,\mathrm{M}$. Calculez la molarité et le titre de la solution d’oxydant.

Un échantillon de $0,320\,\mathrm{g}$ d’un composé ionique contenant des ions bromures ($\ce{Br-}$) est dissous dans l’eau. A cette solution, on ajoute du $\ce{AgNO3}$ en excès. Si la masse du précipité de $\ce{AgBr}$ formé est de $0,6964\,\mathrm{g}$, quel est le pourcentage massique de brome dans le composé initial?

Le laiton est un alliage de cuivre et de zinc. Le pourcentage de cuivre dans le laiton peut être déterminé en ajoutant de l'acide nitrique concentré, puis en utilisant un colorimètre pour analyser l'intensité de couleur (bleu) du nitrate de cuivre ($II$) formé. L’équation du processus est la suivante:
$\ce{4 HNO3 + Cu -> Cu(NO3)2 + 2 NO2 + 2 H2O}$
La chemise en laiton d’une cartouche (cf. image), de masse égale à $6,7\,\mathrm{g}$, est traitée avec de l’acide nitrique. Une fois la réaction terminée et après dilution, on récupère $200\,\mathrm{mL}$ d'une solution de $\ce{Cu(NO3)2}$ de concentration égale à $0,4\,\mathrm{M}$.
Déterminer la masse de cuivre contenue dans la chemise, ainsi que son pourcentage.

Cartouche en laiton

Résumé du chapitre sur les concentrations

Quels sont les paramètres employés dans ce chapitre ?

Paramètre	Unité de mesure
Masse	$\mathrm{g}$
Quantité de matière	$\mathrm{mol}$
Volume	$\mathrm{L}$ ou $\mathrm{mL}$
Titre	$\mathrm{g/mL}$ ou $\mathrm{g/L}$
Molarité	$\mathrm{mol/L = M}$

Comment peut-on passer des grammes aux moles ?
Il faut connaître la masse d'une mole = masse molaire.

$$ moles=\frac{masse}{masse\,molaire}\Rightarrow \mathrm{\frac{g}{\frac{g}{mol}}=g\cdot \frac{mol}{g}} $$

Comment peut-on déterminer la molarité d'une solution à partir des moles de soluté ?
Il faut connaître le volume de la solution.

$$ molarité=\frac{moles}{volume}\Rightarrow \mathrm{\frac{mol}{L}} $$

Comment peut-on déterminer le volume d'une solution à partir de sa molarité ?
Il faut connaître la quantité en moles de soluté.

$$ volume=\frac{moles}{molarité}\Rightarrow \mathrm{\frac{mol}{\frac{mol}{L}}=mol\cdot \frac{L}{mol}=L} $$

Comment peut-on déterminer les moles de soluté à partir de la molarité de la solution ?
Il faut connaître le volume de la solution.

$$ moles=volume\cdot molarité\Rightarrow \mathrm{L\cdot \frac{mol}{L}=mol} $$

Comment peut-on passer du titre à la molarité d'une solution ?

$$ molarité=\frac{titre}{masse\,molaire}\Rightarrow \mathrm{\frac{\frac{g}{L}}{\frac{g}{mol}}=\frac{g}{L}\cdot \frac{mol}{g}=\frac{mol}{L}} $$

Comment peut-on passer de la molarité au titre d'une solution ?