L'équilibre chimique

Dans ce chapitre, nous abordons le concept d'équilibre chimique, un état où la composition du système reste stable, malgré des changements continus à l'échelle microscopique.
Avant d'explorer cette notion d'équilibre, nous examinerons les questions suivantes :
Pourquoi une réaction est-elle spontanée ? Dans quelles conditions peut-elle l'être ou ne pas l'être ?
Une réaction chimique se poursuit-elle toujours jusqu'à l'épuisement des réactifs ?
Une réaction chimique peut-elle être réversible ?
L'objectif de ce chapitre est de répondre à ces questions et d'étudier les réactions caractérisées par une situation d'équilibre.
Les réponses fournies marqueront une différence notable entre le programme de la 2ème année et celui de cette année.

Rappels de thermochimie

Enthalpie

La plupart des réactions chimiques ont lieu à pression et températures constantes, comme celles imposées par les conditions atmosphériques (à l'air libre) ¹. Aux conditions de pression constante, la variation d'enthalpie $\Delta H $ correspond à la chaleur $Q$ échangée entre le système et son environnement. $$ \Delta H = Q_p $$

où $Q_p$ est la chaleur à pression constante. Si la réaction est exothermique (dégagement de chaleur du système vers l'environnement), la $\Delta H $ est négative, alors que pour une réaction endothermique elle est positive.

Type de réaction	Signe de $\Delta H$
Exothermique	$-$
Endothermique	$+$

On peut aussi affirmer que, dans le cas d'une réaction exothermique, les produits ont une enthalpie plus faible que les réactifs. Cela signifie que les produits sont plus stables que les réactifs ².

Cela nous pousse à conclure qu'une réaction exothermique est plus probablement spontanée qu'une réaction endothermique, car, au bout d'une réaction exothermique, l'on obtient des substances plus stables et donc favorisées.

Toutefois, l'échange de chaleur n'est pas le seul critère pour déterminer si une réaction est spontanée ou si elle ne l'est pas. Par exemple, lorsque la glace fond, le processus est endothermique et spontané.

$$ \ce{H2O_{(s)} -> H2O_{(l)}} \qquad \Delta H^{o} = +6.01\,[\mathrm{kJ/mol}] $$

Cet exemple montre que le signe de $\Delta H$ seul ne permet pas de prédire la spontanéité d'une réaction. la thermodynamique nous permettra de déterminer si une transformation est spontanée ou non pour des conditions données.

Dans la table ci-dessous, nous trouvons des exemples de transformations spontanées et non spontanées.

Spontané	Non spontané
La glace fond à température ambiante.	La glace solidifie à température ambiante.
Le sodium métallique réagit avec l'eau pour former de l'hydroxyde de sodium et du dihydrogène.	L'hydroxyde de sodium réagit avec l'hydrogène pour produire du sodium métallique et de l'eau.
La corrosion du fer à température ambiante.	La transformation de la rouille en fer métallique à température ambiante.

Thermodynamique

La thermodynamique est l'étude de l'énergie et de ses transformations. Dans le chapitre sur la thermochimie, nous nous sommes concentrés sur les transferts de chaleur au cours des réactions chimiques. Nous allons développer d'autres aspects des transferts d'énergie dans ce chapitre.

Entropie

Le critère le plus général est l'augmentation du désordre total (système + environnement) qui a toujours lieu au cours d'une réaction spontanée.

Supposons que vous construisiez un château de cartes. Ce processus n'est pas spontané car il nécessite un apport d'énergie de votre part. Les cartes, une fois empilées sur la table, ont une énergie potentielle élevée et sont disposées de manière ordonnée, avec un faible degré de désordre.

Maintenant, imaginez qu'un courant d'air renverse votre château de cartes. Ce processus est spontané car les cartes se retrouvent étalées sur la table sans intervention. Dans cette nouvelle disposition, les cartes ont une énergie potentielle plus basse et sont placées de manière désordonnée, avec un degré de désordre élevé.

Un processus spontané suit donc naturellement deux tendances :

Le système évolue spontanément vers un état d'énergie plus faible.
Le système évolue spontanément vers un état plus désordonné.

Comment est-il possible de prédire s'il y a augmentation du désordre total lors d'une réaction chimique ?

Si la réaction est exothermique, cela signifie que de l'énergie, sous forme de chaleur, est cédée par le système à l'environnement. Le désordre augmente, car l'énergie n'est plus confinée dans le système, mais elle est dispersée dans un espace bien plus grand.

Si le nombre de moles augmente au cours de la réaction, là aussi, le désordre augmente.

Si le nombre de moles reste inchangée, mais le nombre de moles de gaz augmente, là encore, le désordre a augmenté. Les molécules de gaz sont en effet bien plus désordonnées que les molecules de solide ou liquide.

Prenons la réaction suivante:
$$ \ce{2HCl_{(aq)} + CaCO3_{(s)} -> CaCl2_{(aq)} + H2O_{(l)} + CO2_{(g)}} $$

Le nombre de moles ne varie pas de gauche à droite: toujours $=3$. Par contre, la réaction produit $1$ mole de gaz: le désordre a donc augmenté.

Voici l'exemple de la combustion de l'essence:

$$ \ce{2 C8H18_{(l)} + 25 O2_{(g)} -> 16 CO2_{(g)} + 18 H2O_{(l)}} $$

Cette fois-ci, on observe une augmentation du nombre de moles en allant de gauche à droite. De plus, cette réaction est une combustion: il y a donc dégagement de chaleur, qui est transférée à l'environnement sous forme d'énergie mécanique (la moteur se met en mouvement), mais aussi de chaleur (le moteur chauffe).
Les critères donnés ci-dessus sont satisfaits. Cette réaction est donc spontanée.
Les chimistes utilisent le terme entropie ($S$) pour mesurer le désordre provoqué par l'augmentation du nombre de moles et, en particulier, de moles de gaz.
Globalement, l'augmentation du désordre total permet d'expliquer la spontanéité d'une réaction chimique.

Énergie libre

Afin de tenir compte de tous les termes permettant de mesurer l'augmentation du désordre, les chimistes ont introduit une nouvelle fonction d'état, l'énergie libre de Gibbs ($G$) ou simplement l'énergie libre. La variation de l'énergie libre ($\Delta G_{\mathrm{r}}$) pour une réaction chimique est exprimée comme suit:

$$ \Delta G_{\mathrm{r}} = \Delta H_{\mathrm{r}} - T \Delta S_{\mathrm{r}} $$

où $\Delta H_{\mathrm{r}} = Q_p$, $T$ est la température du système, $\Delta S_{\mathrm{r}}$ est la variation d'entropie.
Une réaction est spontanée si

$$ \Delta G_{\mathrm{r}} < 0 $$

Voyons pourquoi, dans les paragraphes suivants.

Réaction endothermique spontanée

Réaction endothermique: $\Delta H_{\mathrm{r}} > 0$. Le premier critère n'est donc pas satisfait.
Si l'augmentation du désordre lié à l’augmentation du nombre de moles ou à la formation de moles de gaz est suffisant pour contrecarrer le terme $\Delta H_{\mathrm{r}}$ positif, alors la réaction sera spontanée de gauche à droite ($\Delta G_{\mathrm{r}}< 0$).
C'est le cas de l'exemple ci-dessous. $$ \ce{Ba(OH)2\cdot 8 H2O_{(s)} + 2 NH4Cl_{(s)} -> 2 NH3_{(g)} + 8 H2O_{(l)} + BaCl2\cdot 2H2O_{(s)}} $$

Réaction exothermique spontanée

Réaction exothermique: $\Delta H_{\mathrm{r}} < 0$. Le premier critère est donc satisfait.
Admettons, comme dans le cas ci-dessous, qu 'il y ait diminution du désordre à cause d'une diminution du nombre de moles.

$$ \ce{2Al_{(s)} + 3 I2_{(s)} -> 2 AlI3_{(s)}} $$

Cette réaction est spontanée de gauche à droite ($\Delta G^\circ_{\mathrm{r}} < 0$): on en déduit que la diminution du nombre de moles est plus que compensée par la quantité de chaleur dégagée.

Tableau récapitulatif

	Réaction endothermique $\Delta H^\circ_{\mathrm{r}} > 0$	Réaction exothermique $\Delta H^\circ_{\mathrm{r}} < 0$
$\Delta S^\circ_{\mathrm{r}} > 0$	spontanée à hautes températures non spontanée à basses températures	toujours spontanée
$\Delta S^\circ_{\mathrm{r}} < 0$	jamais spontanée	spontanée à basses températures non spontanée à hautes températures

Calcul de la $\Delta G^\circ_{\mathrm{r}}$

Nous effectuerons les calculs dans les conditions standard (indiquée par l'exposant $^\circ$), c'est à dire pour $1$ mole de chaque composé.

Exercice:

Soit la réaction de décomposition de la calcite :

$$ \ce{CaCO3_{(s)} -> CaO_{(s)} + CO2_{(g)}} $$

Calculez, à partir des tables CRM, $\Delta H^\circ_{\mathrm{r}}$ et $\Delta S^\circ_{\mathrm{r}}$, à l'aide des $\Delta H^\circ_{\mathrm{f}}$ et des $S^\circ$.

$$ \begin{align} &\Delta H^\circ_{\mathrm{r}}=\Delta H^\circ_{\mathrm{f}}(\ce{CaO})+\Delta H^\circ_{\mathrm{f}}(\ce{CO2})-\Delta H^\circ_{\mathrm{f}}(\ce{CaCO3}) \\ &\Delta H^\circ_{\mathrm{r}} = -635-394+1207= 178\,\mathrm{kJ} \\ \\ &\Delta S^\circ_{\mathrm{r}}=S^\circ(\ce{CaO})+S^\circ(\ce{CO2})-S^\circ(\ce{CaCO3}) \\ &\Delta S^\circ_{\mathrm{r}} = 38+214-92=160\frac{\mathrm{J}}{\mathrm{K}}=0,160\,\frac{\mathrm{kJ}}{\mathrm{K}} \end{align} $$

Calculez, à partir des valeurs obtenues ci-dessus, l’énergie libre de Gibbs $\Delta G^{o}$, à $25\mathrm{^\circ C}$ et dites si le processus sera spontané ou non.

$$ \begin{align} &\Delta G^\circ_{\mathrm{r}} = \Delta H^\circ_{\mathrm{r}} - T \Delta S^\circ_{\mathrm{r}} \\ &\Delta G^\circ_{\mathrm{r}} =178 \,\mathrm{kJ}-298\,\mathrm{K}\times 0,160\,\frac{\mathrm{kJ}}{\mathrm{K}}=130\,\mathrm{kJ} \end{align} $$

La $\Delta G^\circ$ étant supérieure à $0$, la réaction n'est pas spontanée de gauche à droite.
On peut en revanche affirmer que la réaction sera spontanée de droite à gauche. Cette dernière remarque est importante pour la suite de ce chapitre.

L'équilibre chimique

Condition : $\Delta G_{\mathrm{r}}=0$

Jusqu'à présent, nous avons calculé la $\Delta G^\circ_{\mathrm{r}}$ entre les produits et les réactifs dans leur état standard: toutes les pressions des gaz sont considérées à $1\,\mathrm{atm}$ et les molarités des substances en solution égales à $1\,\mathrm{mol\cdot L^{-1}}$.

Notez qu'un équilibre peut se réaliser seulement si $\Delta H^\circ_{\mathrm{r}}$ et $\Delta S^\circ_{\mathrm{r}}$ ont le même signe².

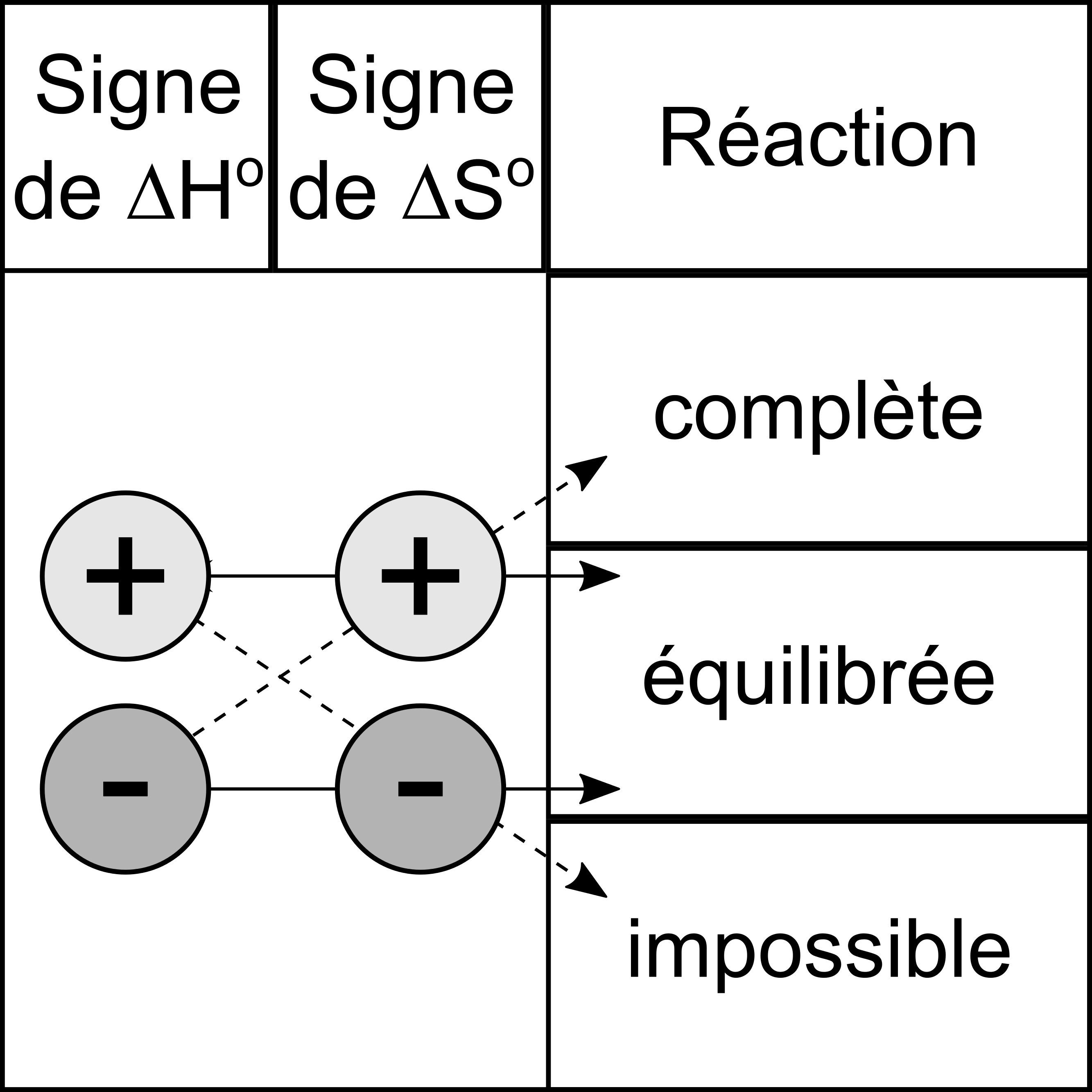
Les signes de $\Delta H^\circ _{\mathrm{r}} $ et de $\Delta S^\circ _{\mathrm{r}} $ sont utiles pour déterminer le type de réaction.

Si on s'éloigne des conditions standard, nous aurons une $\Delta G_{\mathrm{r}}$ qui dépend de la composition du mélange réactionnel et qui représente la différence d'énergie libre aux concentrations présentes à un instant donné, dans le mélange. La $\Delta G_{\mathrm{r}}$ varie donc et peut même devenir égale à $0$.

Que se passe-t-il lorsque la $\Delta G_{\mathrm{r}}=0$ ?

La réaction ne procédera pas de gauche à droite, ni de droite à gauche. On peut dire que la réaction est dans une situation d'équilibre. Lorsque l'équilibre est atteint, les concentrations des réactifs et des produits ne varient plus.

Constante d'équilibre

Dans le tableau ci-dessous sont données les valeurs expérimentales des concentrations à l'équilibre pour la réaction $\ce{H2_{(g)} + I2_{(g)} -> 2HI_{(g)}}$. Ces résultats ont été obtenus à partir de mélanges ayant des compositions initiales différentes.

Mélange	[$\ce{H2_{(g)}}$] $\,\mathrm{mol/L}$	[$\ce{I2_{(g)}}$] $\,\mathrm{mol/L}$	[$\ce{HI_{(g)}}$] $\,\mathrm{mol/L}$
1	$1,14$	$0,12$	$2,52$
2	$0,92$	$0,20$	$2,96$
3	$0,77$	$0,31$	$3,34$
4	$0,92$	$0,22$	$3,08$
5	$0,35$	$0,35$	$2,35$
6	$0,86$	$0,86$	$5,86$

A partir de chacun de ces mélanges, la réaction a évolué jusqu'à l'équilibre, qu'on indiquera par la double flèche.

$$ \ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2HI_{(g)}} $$

Les résultats expérimentaux du tableau ne semblent pas avoir de relation entre eux. Mais, si nous calculons la valeur de la quantité suivante:

$$ K_{\mathrm{c}}=\frac{[\ce{HI}]^2}{\ce{[H2]}\cdot \ce{[I2]}} $$

nous otenons la même valeur dans chaque cas. Ce résultat montre que $K_c$ définit la composition du mélange à l'équilibre et sa valeur est toujours la même. On l'appelle alors constante d'équilibre de la réaction ³.
L'indice $c$ de $K_c$ indique que $K$ est défini en fonctions des concentrations molaires et les crochets $[\,]$ servent justement à indiquer une molarité.

De façon plus générale, on peut appliquer cette relation appelée loi d'action de masse pour n'importe quelle réaction:

$$ \ce{aA + bB \rightleftharpoons cC + dD} $$

où:

$$ K_{\mathrm{c}}=\frac{[\ce{C}]^c \cdot [\ce{D}]^d}{[\ce{A}]^a \cdot [\ce{B}]^b} $$

Remarque: les concentrations des produits purs liquides servant de solvant ou les solides restant non solubilisés sont considérées comme des constantes déjà incluses dans la valeur de la constante d'équilibre, et ne sont pas prises en compte dans son équation quelle que soit leur quantité.

Considérons l'exemple:

$$ \ce{CaCO3_{(s)} \rightleftharpoons CO2_{(g)} + CaO_{(s)}} $$

$K_{\mathrm{c}}=$

On peut aussi définir $K_{\mathrm{p}}$, si les substances à l'équilibre sont à l'état gazeux:

$$ K_{\mathrm{p}}=\frac{p_{\mathrm{C}}^c\cdot p_{\mathrm{D}}^d}{p_{\mathrm{A}}^a\cdot p_{\mathrm{B}}^b} $$

où $p$ indique la pression partielle de chaque gaz ($p_{\mathrm{partielle}} = p_{\mathrm{totale}}\times X $, $X$ étant la fraction molaire de la substance considérée - exemple: $X_A=\frac{n_A}{n_{\mathrm{totale}}}$ est la fraction molaire de $\ce{A}$ et est égale au rapport entre le nombre $n$ de moles de $\ce{A}$ et le nombre total de moles, toute substance confondue).

Interprétation de la constante d'équilibre

Tout en étant prudent lorsque le nombre de moles du système initial est différent de celui du système final, on peut dire que pour une réaction de type: $\ce{aA + bB \rightleftharpoons cC + dD}$ :

Lorsque la valeur de la constante est élevée, par exemple $10^3$, les concentrations de $\ce{C}$ et de $\ce{D}$ sont beaucoup plus grandes que les concentrations de $\ce{A}$ et de $\ce{B}$. On dit que l'équilibre est déplacé à droite, comme dans le cas de la protolyse de $\ce{HClO3}$:

$\ce{HClO3 + H2O \rightleftharpoons H3O+ + ClO3^-} \qquad K_{\mathrm{c}}= 2,8\times 10^4$
Lorsque la valeur de la constante est petite, par exemple $10^{-4}$, les concentrations de $\ce{C}$ et de $\ce{D}$ sont beaucoup plus petites que les concentrations de $\ce{A}$ et de $\ce{B}$. On dit que l'équilibre est déplacé à gauche, comme dans le cas de la protolyse de $\ce{CH3COOH}$ :

$\ce{CH3COOH + H2O \rightleftharpoons H3O+ + CH3COO-} \qquad K_{\mathrm{c}} = 1,1\times 10^{-3}$

Sens d'évolution des réactions

La valeur de la constante d'équilibre permet de savoir si un mélange réactionnel évoluera vers la formation d'une plus grande quantité de produits ou vers sa décomposition en réactifs³.

Avec les données à disposition, nous calculons d'abord le quotient réactionnel $Q_{\mathrm{c}}$: cette grandeur est définie comme la constante d'équilibre, mais avec les concentrations molaires à un stade quelconque de la réaction et très probablement en dehors de l'équilibre.

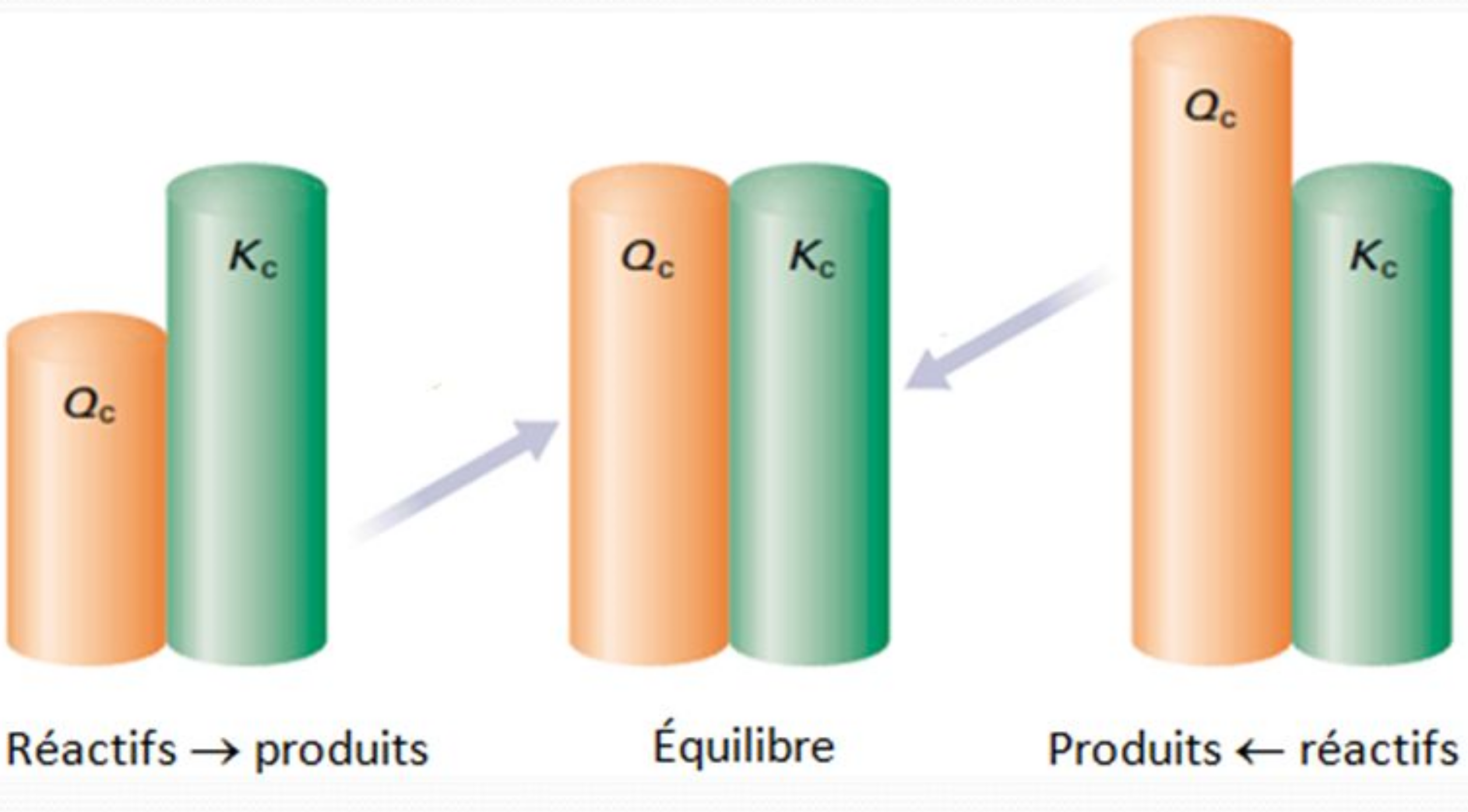
La valeur du quotient réactionnel nous permet de déterminer le sens d'évolution des réactions.

Une réaction aura donc tendance à évoluer vers les produits si $Q_{\mathrm{c}} < K_{\mathrm{c}}$ ou vers les réactifs si $Q_{\mathrm{c}} > K_{\mathrm{c}}$.

Relation énergie libre / équilibre chimique

La thermodynamique nous apprend que la relation entre $\Delta G$ et $\Delta G^o$ est la suivante :

$$ \Delta G_{\mathrm{r}} = \Delta G^o_{\mathrm{r}} + RT \cdot ln(Q_{\mathrm{c}}) $$

où $R$ est la constante des gaz parfaits, $T$ est la température en kelvin et $Q_{\mathrm{c}}$ est le quotient réactionnel.

Par définition, à l'équilibre, $\Delta G_{\mathrm{r}} = 0$ et $Q_{\mathrm{c}} = K_{\mathrm{c}}$. Ainsi :

$$ 0 = \Delta G^o_{\mathrm{r}} + RT \cdot ln(K_{\mathrm{c}}) \quad \Rightarrow \quad \Delta G^o_{\mathrm{r}} = - RT \cdot ln(K_{\mathrm{c}}) $$

$K_{\mathrm{c}}$	$ln(K_{\mathrm{c}})$	$\Delta G^o_{\mathrm{r}}$	Résultat à l'équilibre
> 1	positif	négatif	Les produits sont favorisés
= 1	nul	nul	Ni produits, ni réactifs sont favorisés
< 1	négatif	positif	Les réactifs sont favorisés

Selon cette équation, plus $K_{\mathrm{c}}$ est grand, plus $\Delta G^o$ est négatif. Cette équation permet de déterminer la constante d'équilibre d'une réaction si l'on connaît la variation de l'énergie libre standard, et vice versa.

Cinétique

Le terme cinétique est associé à la vitesse d'une réaction chimique. On imagine bien que tout facteur susceptible de favoriser les rencontres entre particules augmentera la vitesse d'une réaction et l'on vérifie expérimentalement que la vitesse à laquelle se déroule une réaction chimique dépend de :

La nature des réactifs.

La température.

La concentration des réactifs (pour les solutions ou les gaz).

L'état de division (pour les solides et les liquides). Si les réactifs se trouvent sous forme de poudre fine, leur surface de contact est plus grande, les rencontres seront plus fréquentes: il y a plus de collisions efficaces, la réaction se fait beaucoup plus facilement que s'ils se trouvent sous forme de solide compact.

La pression partielle (pour les gaz).

La présence éventuelle d'un catalyseur.

Cinétique et équilibre chimique

Les images suivantes nous permettront de comprendre la relation entre cinétique et équilibre chimique, à travers des simples analogies telles que la guerre de pomme entre un garçon et son voisin⁴.

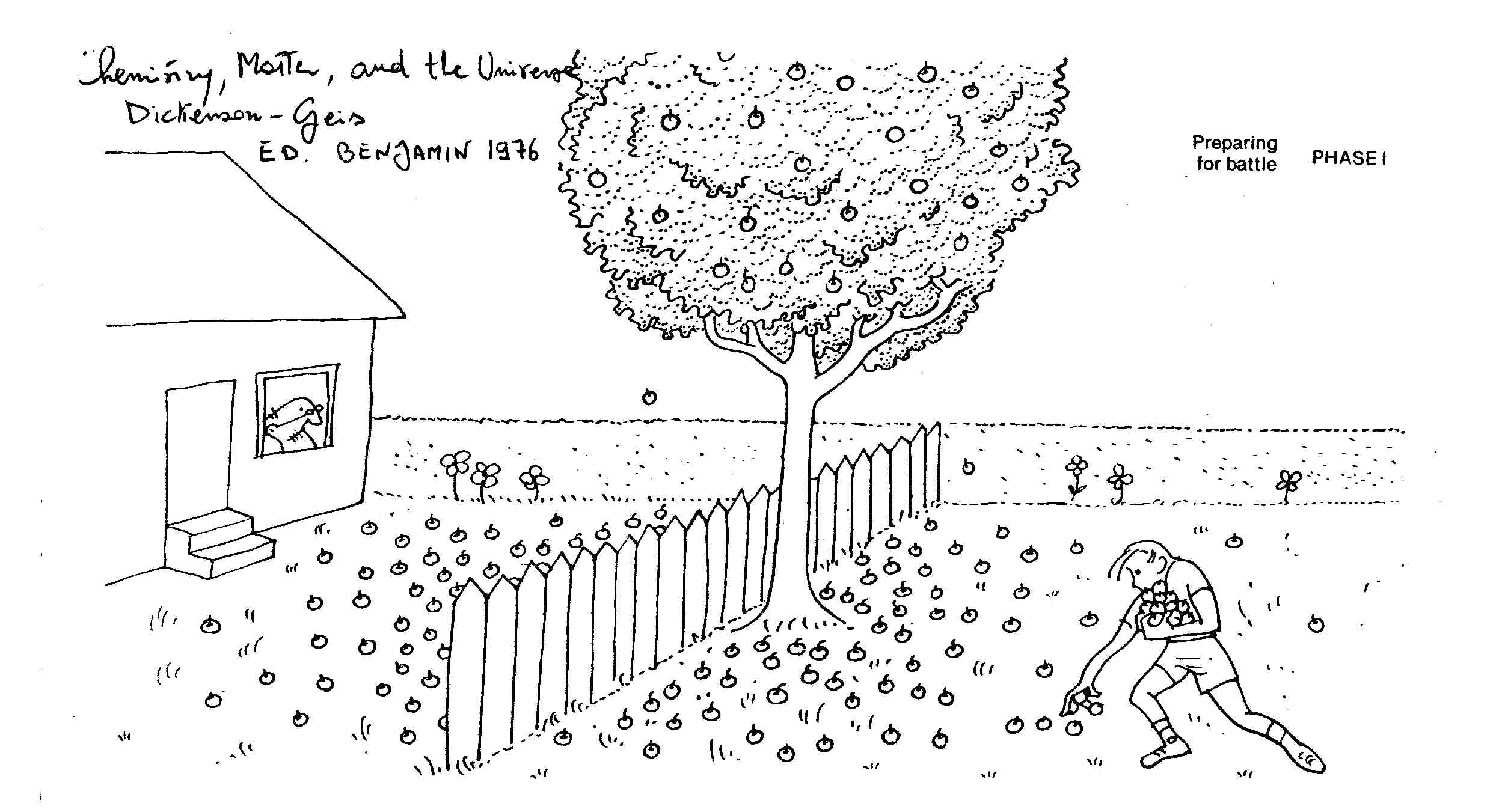
Le garçon ramasse les pommes de son verger.

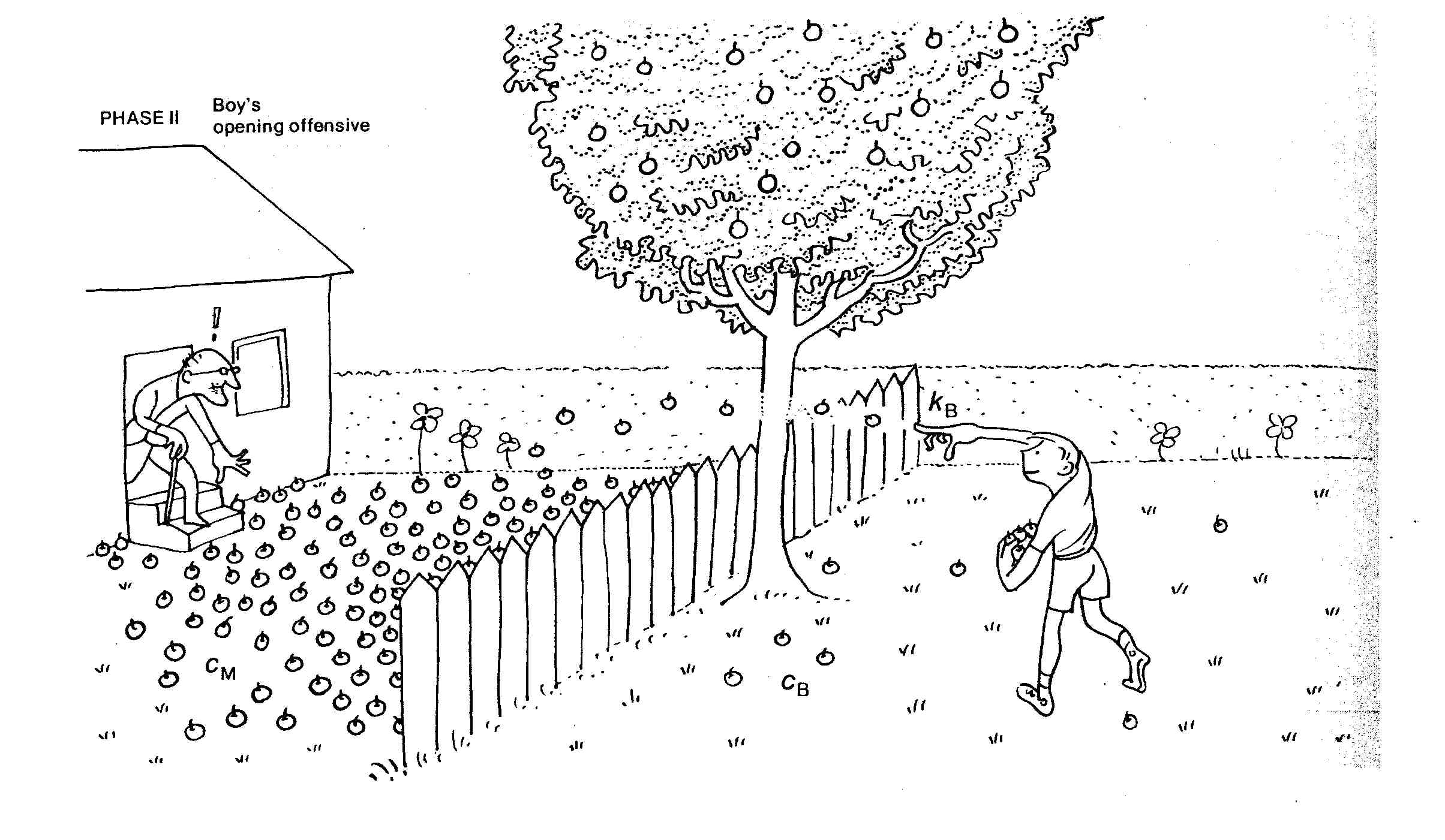
Au lieu de les ranger à la cave, il s'amuse à les jeter chez le voisin, à la vitesse $k_B$.

Le voisin, un monsieur plutôt âgé, ne se laisse pas faire et renvoie les pommes de l'autre coté de la barrière à une vitesse $k_M$.

Un équilibre s'établit lorsque la vitesse globale à laquelle le monsieur lance les pommes équivaut celle du garçon.

La vitesse globale de ce processus (jet de la pomme) est donnée par $v=k\times c$, où $k$ est une constante de vitesse et $c$ une concentration. L'équilibre s'établit lorsque le monsieur, qui est moins rapide ($k_M$ petit), se retrouve avec beaucoup plus de pommes à disposition ($c_M$ grand) et que le garçon, bien que plus rapide ($k_B$ grand), n'a que très peu de pommes à disposition ($c_B$ petit). Dans cette situation, les deux processus s'annulent et les concentrations $c_B$ et $c_M$ ne varient plus: on dit que l'équilibre est atteint.
L’analogie de la « guerre des pommes » est utile pour expliquer les phénomènes d’équilibre qui ont lieu en chimie.
Prenons le cas d’un bêcher d’eau dans un bocal fermé. L'eau s'évapore, le niveau s'abaisse. Au bout d'un certain temps, on constate que le bocal est saturé de vapeurs d'eau, le niveau d'eau reste constant. On dit que l'équilibre évaporation $\ce{\rightleftharpoons}$ condensation est atteint, mais les molécules d'eau à la surface continuent de s'évaporer, tandis que d'autres se condensent : c'est un équilibre dynamique. La vitesse d'évaporation est égale à la vitesse de condensation.

De même dans une réaction chimique :

$$ \ce{aA + bB \rightleftharpoons cC + dD} $$

A et B réagissent ensemble avec la vitesse $v_1$ donnant C et D. Au bout d'un moment, C et D présents réagissent ensemble avec la vitesse $v_2$. Cette réaction étant réversible, on pourra exprimer la vitesse $v_1$ de la réaction directe et la vitesse $v_2$ de la réaction inverse selon :

$$ \begin{align} v_1=k_1\times [\ce{A}]^\alpha \times [\ce{B}]^\beta \\ v_2=k_2\times [\ce{C}]^\gamma \times [\ce{D}]^\delta \end{align} $$

Du point de vue de la cinétique, le système est dit en équilibre si, à une température donnée, la vitesse de la réaction $1$ est égale à celle de la réaction inverse $2$, les concentrations des espèces chimiques du système restent constantes, mais les réactions se font continuellement dans les deux sens.

A l’équilibre : $v_1 = v_2$. Cette équation stipule que l'équilibre chimique est dynamique. Les deux réactions opposées procèdent toujours, mais à la même vitesse.

Evolution d’une réaction au cours du temps.

Evolution des vitesses de réaction au cours du temps.

Soit la réaction qui évolue vers l'état d'équilibre décrit par l'équation : $\ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2HI_{(g)}}$

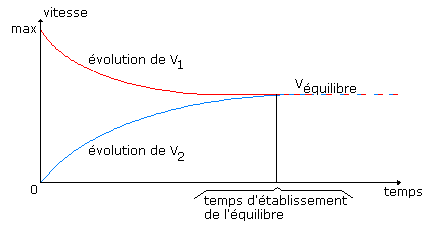
La vitesse $v_1$ diminue, alors que la vitesse $v_2$ augmente: l'équilibre s'établit à l'instant où $v_1=v_2$.

Au moment où l'on mélange $\ce{H2}$ et $\ce{I2}$, $v_1$ est maximum et $v_2$ est nulle. Au fur et à mesure que la réaction se poursuit, $v_1$ diminue et $v_2$ augmente.
Au moment où $v_1 = v_2$ il y a EQUILIBRE.
Les deux réactions se poursuivent alors à des vitesses égales et constantes sans changement dans les concentrations respectives des constituants $\ce{H2}$, $\ce{I2}$, $\ce{HI}$.

Evolution des concentrations au cours du temps.

A l'équilibre, les concentrations tendent vers une valeur constante. Voici pour $\ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2HI_{(g)}}$, la variation de concentration en fonction du temps, jusqu'à l'équilibre.

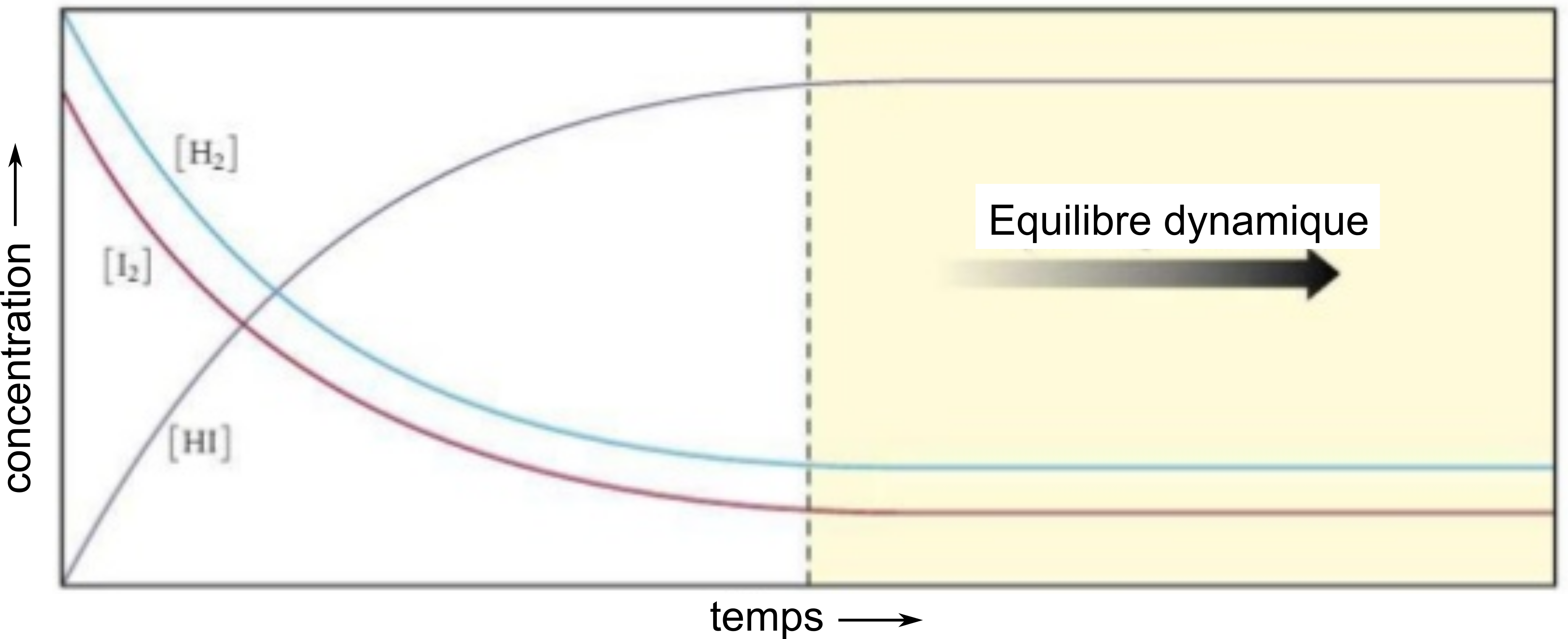
Au cours de la réaction, à partir des concentrations initiales données dans le graphique, les concentrations varient jusqu'à l'équilibre.

Exercice:

Parmi les graphiques (simplifiés) ci-dessous, lesquels peuvent correspondre à une réaction du type : $\ce{A + B \rightleftharpoons C + D}$ ?

Expliquez pourquoi des graphiques différents peuvent correspondre à une même équation.

Si un graphique ne correspond pas à l'équation donnée, trouvez l'équation chimique qui peut bien s'adapter à ce graphique ?

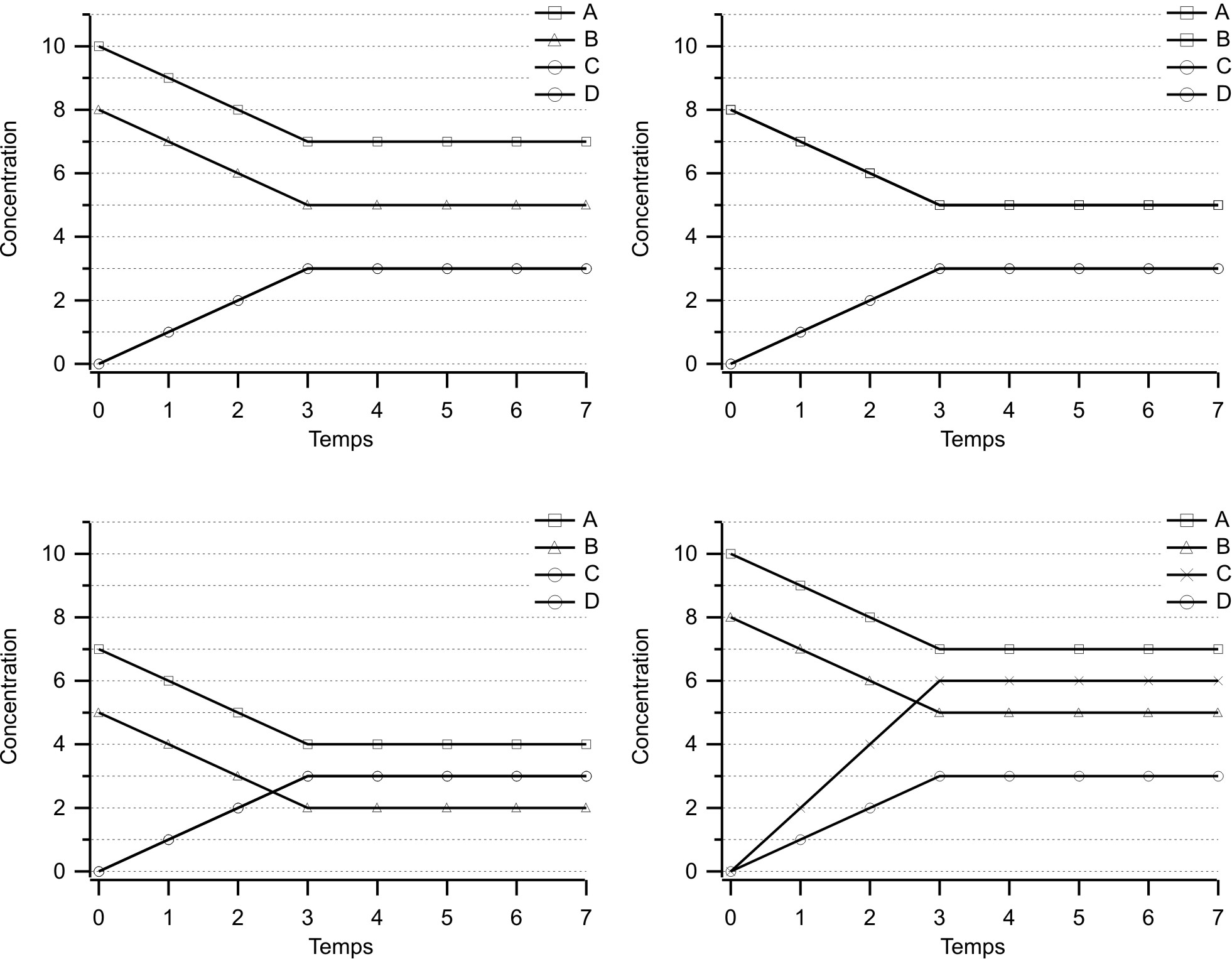
Quels sont les graphiques qui peuvent correspondre à l'équation ? $\ce{A + B \rightleftharpoons C + D}$

Détermination des concentrations molaires à l'équilibre

Voici un problème typique: à la température de $450\mathrm{^\circ C}$, la $K_{\mathrm{c}}$ de la réaction $\ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2HI_{(g)}}$ est égale à $49$. Au départ, la concentration de chaque réactif est de $0,01\,\mathrm{mol}\cdot L^{-1}$ et le volume est de $10\,\mathrm{L}$. Déterminez les concentrations à l'équilibre pour chaque espèce présente dans le mélange réactionnel.

	$\ce{H2_{(g)}}$	$\ce{I2_{(g)}}$	$\ce{2HI_{(g)}}$
proportions	$1$	$1$	$2$
moles initiales $=mol_i$	$0,1$	$0,1$	$0$
variation $=mol_v$	$-x$	$-x$	$2x$
moles à l'équilibre $=mol_e$	$0,1-x$	$0,1-x$	$0+2x$

On introduit les molarités à l'équilibre : $$ K_{\mathrm{c}}=\frac{\left(\frac{2x}{10}\right)^2}{\left(\frac{0,1-x}{10}\right)\cdot \left(\frac{0,1-x}{10}\right)} $$

et on isole le $x$. Notez que l'équation mathématique est du deuxième degré: il s'agira donc de selectionner le $x$ qui est compatible avec les quantités initiales. A vous d'exercer les maths !
(Résultat $\,=0,078\,\mathrm{mol}$ pour $x$).

Exercice:

Soit la réaction de dissociation : $\ce{A2_{(g)} \rightleftharpoons 2A_{(g)}}$

On a un système à l'équilibre dont le nombre de moles est donné dans la première ligne du tableau ci-dessous. Calculez le nombre de moles au départ.

Calculez la $K_{\mathrm{c}}$.

En modifiant le volume du récipient, on déplace cet équilibre, et on obtient une nouvelle répartition des moles (cf. deuxième ligne du tableau ci-dessous). En utilisant ces valeurs, calculez $V_2$.

	nombre de moles de $\ce{A2}$	nombre de moles de $\ce{A}$	Volume / $\mathrm{L}$
équilibre 1	$5$	$10$	$4$
équilibre 2	$7$	$6$	$V_2$

Déplacement de l'équilibre (Principe de Le Châtelier)

Principe de Le Châtelier: Si une réaction chimique à l'équilibre est soumise à un changement de conditions (pression, température, concentration) qui perturbe cet équilibre, alors la réaction évolue vers un nouvel état d'équilibre de telle manière que la cause du déséquilibre soit compensée dans la mesure du possible.

Certains facteurs peuvent influencer un état d'équilibre et le déplacer soit vers le système initial, soit vers le système final. Ces facteurs sont principalement :

Les variations de CONCENTRATION d'une ou de plusieurs substances en présence à l'équilibre.
Les variations de TEMPÉRATURE .
Les variations de PRESSION si une ou plusieurs substances en présence à l'équilibre sont à l'état gazeux.

Influence de la concentration

Exemple : $\ce{BiCl3 + H2O \rightleftharpoons BiOCl v + 2 HCl}$

Si l'on augmente la concentration de $\ce{H2O}$, le système cherche à la faire disparaître ; l'équilibre se déplace alors vers la droite jusqu'au nouvel équilibre. Les concentrations du système initial diminuent et celles du système final augmentent.

D'ailleurs, selon la loi d'action de masse $K_{\mathrm{c}} = $

Si la concentration en eau augmente, pour que $K_{\mathrm{c}} $ qui est une constante le reste, il faut que la concentration en $\ce{HCl}$ augmente aussi.
En revanche, on observe un déplacement vers la gauche en augmentant la concentration de $\ce{HCl}$.

Exercice:

Dans la réaction de transformation du sucre $\ce{C6H12O6}$ en éthanol, qu'arrive-t-il si on ajoute du sucre ? Et si on agite la réaction pour éliminer le gaz carbonique ?

$$ \ce{C6H12O6 \rightleftharpoons 2 C2H5OH + 2 CO2} $$

Influence de la température

Pour déterminer l'influence de la température, il est nécessaire de savoir si une réaction est exo ou endothermique.

Une réaction exothermique est une réaction qui dégage de l'énergie sous forme de chaleur. Les produits formés sont plus stables que les réactifs.

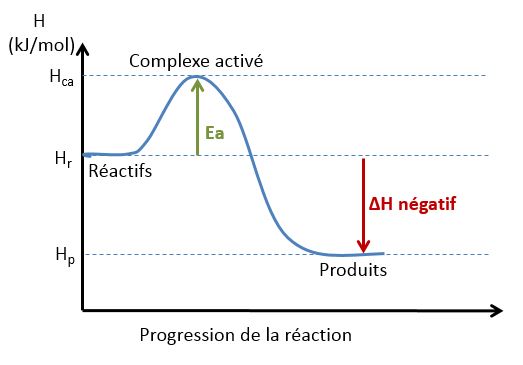
Profil de l'enthalpie pour une réaction exothermique: la $\Delta H_{\mathrm{r}}$ est négatif.

Une réaction endothermique est une réaction à qui il faut fournir de l'énergie sous forme de chaleur pour qu'elle ait lieu.

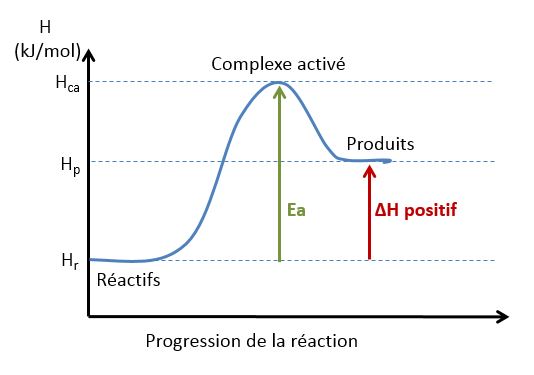
Profil de l'enthalpie pour une réaction endothermique: la $\Delta H_{\mathrm{r}}$ est positif.

Dans les graphiques ci-dessus, $E_a$ indique l'énergie d'activation qui représente l'énergie dont le système a besoin, en plus de son énergie potentielle initiale, pour activer ses réactifs leur permettant de faire la réaction. Le système doit franchir cette barrière d'énergie même si à la fin de la réaction, il dégage de l'énergie à l'extérieur.

Cette énergie d'activation provient de la transformation d'une partie ou de la totalité de l'énergie cinétique que le système acquiert lors des collisions des molécules.
Au sommet de la courbe énergétique se trouve l'état de transition. C'est l'état où les molécules de départ "voient" leurs liaisons se rompre, et où les produits nouveaux "voient" leurs liaisons se former, formant ainsi un complexe activé $\ce{A*}$.

Exemple: $\quad\ce{2 NO2 \rightleftharpoons N2O4} + 59 \,\mathrm{kJ}$

Dans le cas où la pression du système est constante, si l'on augmente la température du système, ce dernier va s'y opposer en absorbant la chaleur qu'on lui fournit. On favorise alors le sens endothermique. Si l'on diminue la température, on favorise le sens exothermique.

Remarque: La constante d'équilibre reste constante si on perturbe la concentration ou la pression des participants. Ce n'est plus le cas lorsque l'on change la température de la réaction.

Influence de la pression (par un changement de volume)

Comptez les molécules présentes à chaque étape !

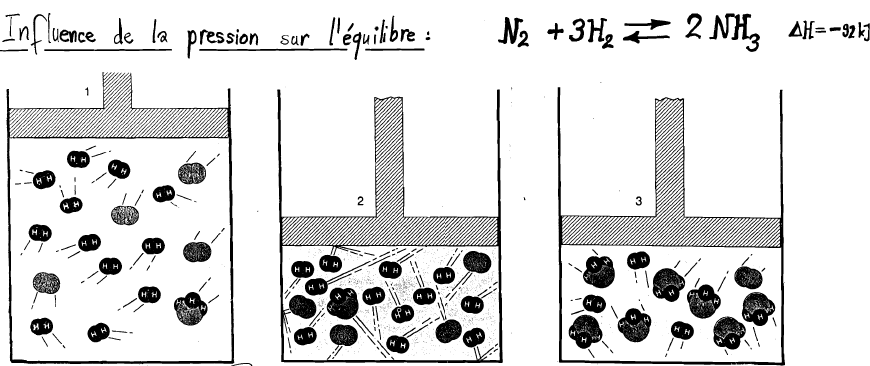
L'effet de la pression sur l'équilibre d'une réaction à l'état gazeux.

Début :

Augmentation de la pression (par une diminution de moitié du volume) :

L’équilibre s’établit à nouveau. Quel changement observe-t-on ?

$$ K_{\mathrm{c}} = \frac{[\ce{NH3}]^2}{[\ce{N2}]\cdot[\ce{H2}]^3} $$
Le système réagit à l’augmentation de la pression (obtenue en diminuant le volume) en essayant de rétablir l’équilibre. La pression d'un gaz dépend directement du nombre de particules, donc du nombre de moles. L'augmentation de la pression déplace donc l'équilibre du côté où il y a le moins de moles de gaz et vice versa. Dans notre exemple, si l'on augmente la pression, l'équilibre se déplacera à droite (moins de moles de gaz) ; si l'on abaisse la pression l'équilibre se déplacera à gauche (plus de moles de gaz).

A noter que:

L'addition d'un gaz inerte à volume constant varie la pression totale, alors que les pressions partielles (=concentrations) des gaz demeurent constantes. Aucun effet sur l'équilibre n'a donc lieu, dans ces conditions.
Si on change la température à volume constant, cela implique également une variation de la pression (car les particules « bougent davantage »). Une telle situation est donc imprévisible, car deux paramètres sont changés simultanément.

Catalyse

Un catalyseur est toute substance ajoutée en petite quantité à une réaction pour en modifier la vitesse ($v_1$ ou $v_2$) sans qu'elle n'apparaisse dans les produits de réaction. On le récupère en général intégralement à la fin de la réaction. Les catalyseurs sont très variés : ions, métaux, enzymes, etc.

Comment agit un catalyseur ?

Il y a deux manières permettant d'accélérer la vitesse d'une réaction :

augmenter l'énergie cinétique des molécules en augmentant la température.
diminuer l'énergie d'activation.

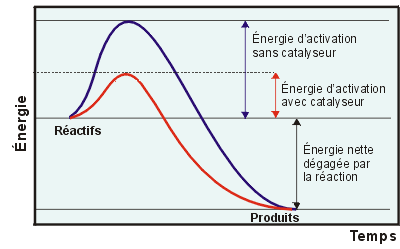
Un catalyseur agit sur la vitesse d'une réaction, en alterant l'énergie d'activation.

C'est la diminution de l'énergie d'activation qui est souvent choisie en utilisant un catalyseur. On peut aussi faire ralentir ou "désactiver" une réaction non désirée en ajoutant un catalyseur "inhibiteur". Le pot catalytique monté sur les véhicules automobiles contient environ deux grammes de platine et de rhodium finement divisés, présentant alors une surface de $8000\,m^2$.

Un catalyseur est sans effet sur $K_{\mathrm{c}}$ ou $K_{\mathrm{p}}$ et reste intact en fin de réaction, donc réutilisable et en petite quantité.

Lorsqu’un catalyseur est utilisé pour accélérer une transformation, on dit que celle-ci est catalysée. Un catalyseur modifie le mécanisme réactionnel de la réaction étudiée, c’est-à-dire la nature des étapes permettant de passer des réactifs aux produits. En aucun cas, il ne pourra modifier le sens d’évolution d’un système, ni son état d’équilibre.

Un catalyseur change uniquement la cinétique de la réaction chimique considérée. Cet aspect est important: la quantité de produit que l'on obtiendra à l'équilibre est la même que si on n'avait pas employé de catalyseur. Mais, cette quantité de produit sera obtenue dans un laps de temps bien plus court.

Un même catalyseur ne peut pas être efficace pour toutes les réactions. En général, un catalyseur catalyse une réaction déterminée et une réaction donnée ne peut être catalysée que par un nombre restreint de catalyseurs. On dit qu’un catalyseur est spécifique d’un type de réaction. Un catalyseur peut également être sélectif si, à partir d’un système initial susceptible d’évoluer selon plusieurs réactions, il accélère préférentiellement l’une d’elles.
La plupart des procédés de synthèse industriels emploient des catalyseurs. Leur utilisation permet une augmentation de la vitesse de réaction et évite aux entreprises des coûts énergétiques trop importants. En effet, une hausse de la température du milieu a le même effet cinétique que l’utilisation d’un catalyseur. Cependant, le coût d’une élévation de température est nettement plus élevé, c’est pourquoi le choix du catalyseur est financièrement plus approprié.
L’importance industrielle et économique des catalyseurs en fait aujourd’hui un des thèmes le plus étudiés dans la recherche.
On pourrait aussi ajouter que, pour une réaction exothermique, une hausse de température diminue la quantité obtenue de produit, ce qui n'est pas souhaitable.

Soit la réaction $\ce{A + 3B \rightleftharpoons 2C} \quad \Delta H_{\mathrm{r}} = +50\,\mathrm{kJ}$: interprétez chacune des trois situations qui s'éloignent de la situation de référence, définie par les conditions ambiantes :

addition d'un catalyseur aux conditions ambiantes
hausse de température (sans catalyseur et pour une pression de $1\,\mathrm{atm}$)
diminution de la pression (sans catalyseur et pour une température de $25\mathrm{^\circ C}$)

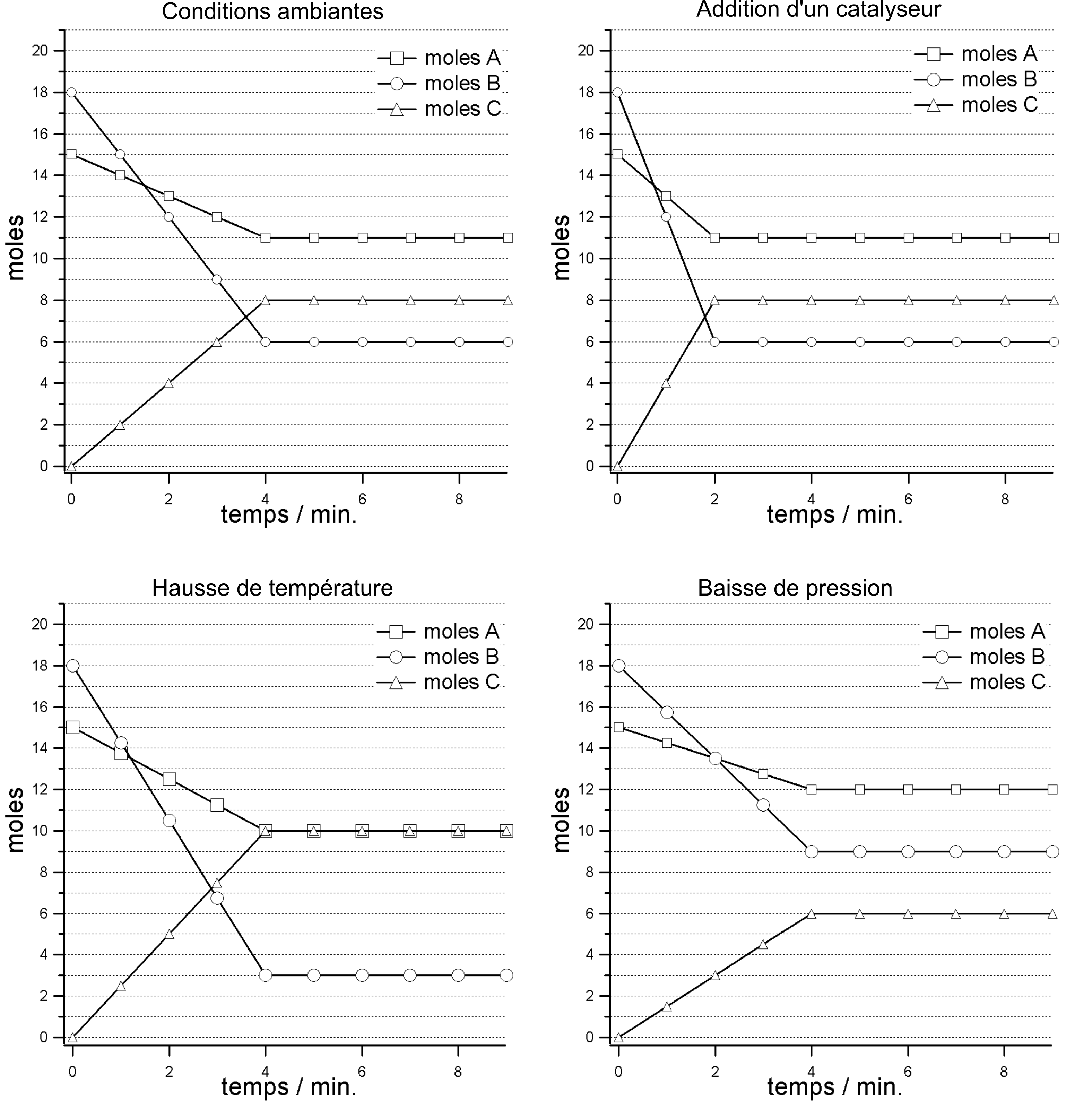
Les effets de plusieurs facteurs sur l'équilibre d'une réaction chimique.

Exercices SERIE Equilibre chimique

Soit la réaction : $\ce{NH4NO3_{(s)} -> NH4+_{(aq)} + NO3^{-}_{(aq)}} $

Calculez $\Delta H^\circ_{\mathrm{r}} $ and $\Delta S^\circ_{\mathrm{r}} $ de cette réaction.

Calculez $\Delta G^\circ_{\mathrm{r}} $ pour cette réaction à $25\mathrm{^\circ C}$, et expliquez pourquoi $\ce{NH4NO3}$ se dissout spontanément aux conditions ambiantes.

Sans effectuer aucun calcul, dites si l'entropie du système augmente ou diminue au cours du processus et justifiez:

l'oxydation de l'azote: $\ce{N2_{(g)} + 2O2_{(g)} -> 2NO2_{(g)}}$

la sublimation de la glace carbonique: $\ce{CO2_{(s)} -> CO2_{(g)}}$

le refroidissement de l'eau de $50\mathrm{^\circ C}$ à $4\mathrm{^\circ C}$

Calculez la température à partir de laquelle la réduction de l'oxyde de fer ($\ce{III}$) en fer par le carbone, selon la réaction $\ce{2Fe2O3_{(s)} + 3C_{(s)} -> 4Fe_{(s)} + 3CO2_{(g)}}$ devient thermodynamiquement possible.

Donnez l'expression de la constante d'équilibre $K_{\mathrm{c}}$ pour les réactions suivantes :

$\ce{N2O4_{(g)} \rightleftharpoons 2 NO2_{(g)} }$

$\ce{N2_{(g)} + 3 H2_{(g)} \rightleftharpoons 2 NH3_{(g)}}$

Pour la réaction $\ce{SO3_{(g)} \rightleftharpoons SO2_{(g)} + 1/2 O2_{(g)}}$, à $100\mathrm{^\circ C}$, $K_{\mathrm{c}}$ est de $4,07\times 10^{-3}$. Calculez $K_{\mathrm{p}}$ à la même température.

Soit la réaction : $\ce{N2_{(g)} + O2_{(g)} \rightleftharpoons 2 NO_{(g)}} \quad \Delta H^\circ_{\mathrm{r}}>0$ .

$K_{\mathrm{c}}$ à l'équilibre est = $4,8.10^{-3}$ à température ambiante. Que nous dit ce chiffre ?

À température ambiante, y a-t-il beaucoup de $\ce{NO}$ formé ?

Soit la réaction : $\ce{COCl2_{(g)} \rightleftharpoons CO_{(g)} + Cl2_{(g)} }$ $K_{\mathrm{p}}=116$. Calculez $p_{\ce{COCl2}}$ à l'équilibre sachant que $p_{\ce{CO}}$ = $80\,\mathrm{atm}$ et $p_{\ce{Cl2}}$ = $130\,\mathrm{atm}$.

Soit la réaction : $\ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2 HI_{(g)}}$. On remplit un réacteur de $10$ litres avec $0,5\,\mathrm{mol}$ de $\ce{H2}$ et $0,5\,\mathrm{mol}$ de $\ce{I2}$ à $448\mathrm{^\circ C}$. La constante $K_{\mathrm{c}}$ à cette température est de $50$.

Calculez les molarités ($\,\mathrm{mol/L}$) des gaz à l'équilibre.

Calculez les pressions partielles des gaz à l'équilibre.

Dans la réaction d'estérification : acide acétique + éthanol $\rightleftharpoons$ acétate d'éthyle + eau. À $25\mathrm{^\circ C}$, à l'équilibre, on a : $K_{\mathrm{c}} = 4,1$ , [acide] =$0,21\,\mathrm{mol/L} $, [acetate] = $0,91\,\mathrm{mol/L}$ , [eau] = $0,0085\,\mathrm{mol/L}$.

Calculez la concentration à l'équilibre en éthanol.

Soit la réaction : $\ce{2SO2 + O2 \rightleftharpoons 2 SO3} \qquad \Delta H^\circ_{\mathrm{r}} = - 188\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température faut-il se placer pour déplacer cet équilibre à droite ?

Soit la réaction : $\ce{4NH3 + 5O2\rightleftharpoons 4NO + 6H2O} \qquad \Delta H^\circ_{\mathrm{r}} = - 895\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température faut-il se placer pour déplacer cet équilibre à droite ?

Soit la réaction : $\ce{2CO + O2 \rightleftharpoons 2CO2} \qquad \Delta H^\circ_{\mathrm{r}} = - 568\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température le mélange est plus riche en monoxyde de carbone ?

Soit la réaction : $\ce{N2 + O2\rightleftharpoons 2NO} \qquad \Delta H^\circ_{\mathrm{r}} = +184\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température le mélange est plus riche en monoxyde d'azote ?

Soit la réaction : $\ce{2H2O_{g}\rightleftharpoons 2H2 + O2} \qquad \Delta H^\circ_{\mathrm{r}} = +485\,\mathrm{kJ/mol}$. Comment faut-il modifier la pression et la température pour décomposer l'eau selon cette réaction ?

Soit la réaction $\ce{H2 + I2\rightleftharpoons 2HI} \qquad \Delta H^\circ_{\mathrm{r}} = +52\,\mathrm{kJ/mol}$. Comment faut-il modifier la pression et la température pour déplacer cet équilibre vers la droite ?

Soit la réaction s'effectuant dans l'eau: $\ce{As2O3 + 2H2O + 2I2 \rightleftharpoons As2O5 + 4HI}$
Dans quel sens est déplacé cet équilibre si l'on ajoute au mélange une solution d'hydroxyde de sodium ?

Soit la réaction de décomposition de l'hydrogène $\ce{H2 \rightleftharpoons 2H}$. Sachant que la constante $K_{\mathrm{c}}$ régissant cet équilibre a pour valeur $2,6\times 10^{-33}$ à $600\mathrm{^\circ C}$ et $3,1\times 10^{-6}$ à $2000\mathrm{^\circ C}$, cette réaction est endothermique ou exothermique?

Soit la réaction : $\ce{PCl5_{(g)} \rightleftharpoons PCl3_{(g)} + Cl2_{(g)}}$. On chauffe à $250\mathrm{^\circ C}$ une quantité de $\ce{PCl5}$ dans un récipient de $12$ litres. A l'équilibre le récipient contient : $0,21\,\mathrm{mol}$ de $\ce{PCl5}$, $0,32\,\mathrm{mol}$ de $\ce{PCl3}$ et $0,32\,\mathrm{mol}$ de $\ce{Cl2}$.

Calculez la constante d'équilibre $K_{\mathrm{c}}$.

Déterminez le nombre de mole de $\ce{Cl2}$ à l'équilibre lorsqu'une mole de $\ce{PCl5}$ est chauffée à $250\mathrm{^\circ C}$ dans un ballon de $10$ litres.

Même question que la précédante, mais pour un ballon de $1$ litre. Les résultats sont-ils en accord avec le principe de Le Châtelier ?

L'explosion est une réaction de combustion violente:

Quels sont les facteurs qui influencent la vitesse de réaction ?

Qu'est-ce qu' un catalyseur ? Quel est son effet sur une réaction ?

Que deviennent les produits dans une réaction exothermique ? Plus stables ou moins stables que les réactifs de départ ?

Quelle est l'unité de la vitesse de réaction ?

La réaction d'estérification est trop lente si on chauffe ensemble seulement un alcool et un acide carboxylique. Que suggérez-vous pour faire accélérer la réaction ?

Soit la réaction de synthèse de l'ammoniac : $\ce{N2_{(g)} + 3 H2_{(g)} \rightleftharpoons 2 NH3_{(g)}}$ $\Delta H^\circ_{\mathrm{r}} = - 92\,\mathrm{kJ}$. Quel sera l'effet produit sur l'équilibre par :

une augmentation de température ?

une augmentation de pression ?

l'introduction d'un catalyseur ?

Quelles sont les conditions de pression et de température à appliquer aux équilibres suivants pour les déplacer à gauche ?

$\ce{2 CO_{(g)} + O2_{(g)} \rightleftharpoons 2 CO2_{(g)}} \qquad\Delta H^\circ_{\mathrm{r}} = - 566\,\mathrm{kJ} $

$\ce{4 NO_{(g)} + 6 H2O_{(g)} \rightleftharpoons 4 NH3_{(g)} + 5 O2_{(g)}} \qquad\Delta H^\circ_{\mathrm{r}} = + 908\,\mathrm{kJ} $

$\ce{PCl5_{(g)} \rightleftharpoons PCl3_{(g)} + Cl2_{(g)}} \qquad\Delta H^\circ_{\mathrm{r}} = + 112\,\mathrm{kJ} $

Soit la réaction : $\ce{As2O3 + 2 H2O + 2 I2 \rightleftharpoons As2O5 + 4 HI}$. Cet équilibre est déplacé à droite par l'adjonction d'une substance étrangère à la réaction. Laquelle et pourquoi ?

L'acide fluorhydrique $\ce{HF}$ est un acide faible.

Donnez son équation de protolyse.

Que deviennent les concentrations des particules en équilibre si l'on ajoute à la solution du fluorure de sodium $\ce{NaF}$ ?

Que faut-il ajouter à une solution aqueuse d'acide nitreux $\ce{HNO2}$ (acide faible) pour que l'acidité de la solution diminue ?

Soit la réaction : $\ce{2 O3_{(g)} \rightleftharpoons 3 O2_{(g)}}$. Déterminez le sens exothermique, sachant que la constante d'équilibre à $300\,\mathrm{K}$ est plus grande que celle à $500\,\mathrm{K}$.

Dans chacune des réactions suivantes: $\ce{A + B \rightleftharpoons C + D}$

$\ce{HCl + O2 \rightleftharpoons Cl2 + H2O}$ $\qquad\Delta H^\circ_{\mathrm{r}} = 32\,\mathrm{kJ} $
$\ce{HCl_{(g)} + H2O_{(l)} \rightleftharpoons H3O+ + Cl-}$ $\qquad\Delta H^\circ_{\mathrm{r}} = -75\,\mathrm{kJ} $
$\ce{SO2_{(g)} + O2_{(g)} \rightleftharpoons SO3_{(g)}}$ $\qquad\Delta H^\circ_{\mathrm{r}} = -92\,\mathrm{kJ} $

Comment l'équilibre est affecté par :

L'augmentation de la concentration en $\ce{A}$ ?

L'addition de $\ce{B}$ ?

L'élimination de $\ce{B}$ ?

Pour avoir plus de $\ce{C}$, faut-il travailler à haute ou basse température ?

Dans la réaction 3, faut-il travailler à haute ou basse pression pour avoir plus de $\ce{SO3}$ ?

Soit la réaction : $\ce{SnO2_{(s)} + 2 H2_{(g)} \rightleftharpoons 2 H2O_{(g)} + Sn_{(s)}}$. La constante $K_{\mathrm{c}}$ est de $1,6$ à $650\,\mathrm{K}$ et de $3,5$ à $800\,\mathrm{K}$. A quelle température faut-il travailler pour obtenir un bon rendement en étain ?

L'hémoglobine ($\ce{Hb}$) fixe l'oxygène pour donner l'oxyhémoglobine :

$$ \ce{Hb + O2 \rightleftharpoons HbO2} \quad\Delta H^\circ_{\mathrm{r}} < 0 $$

Cette formation est plus importante au niveau des tissus ou dans les alvéoles (poumons), sachant que la température est légèrement plus élevée dans les tissus ?

Soit la réaction : $\ce{H2_{(g)}{(g)} + I2_{(g)} \rightleftharpoons 2 Hl_{(g)}}$. $K_{\mathrm{c}}$ à $448\mathrm{^\circ C}$ est de $50,5$. Si nous commençons la réaction à cette température avec respectivement $10^{-2}$, $5,0\times 10^{-3}$ et $1,5\times 10^{-2}\,\mathrm{mol/L}$ en $\ce{HI}$, $\ce{H2}$, et $\ce{I2}$, prévoyez le sens de la réaction pour atteindre l'équilibre.

Soit la réaction : $\ce{SO3_{(g)} \rightleftharpoons SO2_{(g)} + 1/2 O2_{(g)}}$ à $1000\,\mathrm{K}$. $K_{\mathrm{c}}$ est de $4,12\times 10^{-3}$. Les concentrations initiales des participants sont respectivement de $2\times 10^{-3}$, $5\times 10^{-3}$, $3\times 10^{-2}\,\mathrm{mol/L}$, pour $\ce{SO3}$, $\ce{SO2}$, et $\ce{O2}$. Prévoyez le sens de la réaction pour atteindre l'équilibre à cette température.

Soit la réaction : $\ce{PCl5_{(g)} \rightleftharpoons PCl3_{(g)} + Cl2_{(g)}}$. En prenant une mole de $\ce{PCl5}$ soumise à une température de $200\mathrm{^\circ C}$, on obtient, à l'équilibre, sous une pression de $2\,\mathrm{atm}$. la répartition suivante :

$$ \ce{PCl5} : 0,34\,\mathrm{mol} \quad \ce{PCl3} : 0,66\,\mathrm{mol} \quad \ce{Cl2} : 0,66\,\mathrm{mol} $$

Calculez $K_{\mathrm{p}}$.

Calculez la répartition des différentes molécules en $\%$ du total.

Si la même réaction avait eu lieu dans un ballon où la pression totale du mélange à l'équilibre eut été de $0,5\,\mathrm{atm}$, quelle aurait été la répartition des moles du mélange à l'équilibre ?

Ces deux répartitions sont-elles compatibles avec la loi de Le Châtelier ?

Soit la réaction : $\ce{C2H5OH + CH3COOH \rightleftharpoons CH3COOC2H5 + H2O}$. Lorsqu'une mole de $\ce{C2H5OH}$ est mélangée à une mole de $\ce{CH3COOH}$ à température ambiante, le mélange à l'équilibre contient $2/3$ de moles de $\ce{CH3COOC2H5}$ et $2/3$ de mole d'eau.
Le volume est de $1$ litre.

Calculez la constante d'équilibre $K_{\mathrm{c}}$.

Combien de moles d'ester ($\ce{CH3COOC2H5}$) seront-elles formées à l'équilibre si on mélange $3$ moles d'alcool à $1$ mole d'acide ?

En se référant à la question a), décrivez ce qui se passerait et calculez la nouvelle répartition des molécules à l'équilibre, si l'on avait ajouté un déshydratant capable d'absorber $0,5$ moles d'eau.

Bibliographie

Voici quelques liens consultés et/ou repris tels quels. Merci à leurs auteurs pour le précieux partage de ces ressources:

https://fr.wikipedia.org/wiki/Enthalpie_libre ↩
https://www.lachimie.net/index.php?page=38, site consulté en juillet 2019. ↩↩
Chimie, P. Atkins, L. Jones, Ed. De Boeck (2004) ↩↩
Chemistry, matter, and the universe: An integrated approach to general chemistry, R.E. Dickerson, Ed. W. A. Benjamin (1976) ↩

Touches	Action
`?`	Ouvrir l'aide
`n`	Page suivante
`p`	Page précédente
`s`	Rechercher

L'équilibre chimique

Rappels de thermochimie

Enthalpie

Thermodynamique

Entropie

Énergie libre

Réaction endothermique spontanée

Réaction exothermique spontanée

Tableau récapitulatif

Calcul de la $\Delta G^\circ_{\mathrm{r}}$

Soit la réaction de décomposition de la calcite :

Calculez, à partir des tables CRM, $\Delta H^\circ_{\mathrm{r}}$ et $\Delta S^\circ_{\mathrm{r}}$, à l'aide des $\Delta H^\circ_{\mathrm{f}}$ et des $S^\circ$.

Calculez, à partir des valeurs obtenues ci-dessus, l’énergie libre de Gibbs $\Delta G^{o}$, à $25\mathrm{^\circ C}$ et dites si le processus sera spontané ou non.

L'équilibre chimique

Condition : $\Delta G_{\mathrm{r}}=0$

Constante d'équilibre

Interprétation de la constante d'équilibre

Sens d'évolution des réactions

Relation énergie libre / équilibre chimique

Cinétique

Cinétique et équilibre chimique

Evolution d’une réaction au cours du temps.

Evolution des vitesses de réaction au cours du temps.

Evolution des concentrations au cours du temps.

Parmi les graphiques (simplifiés) ci-dessous, lesquels peuvent correspondre à une réaction du type : $\ce{A + B \rightleftharpoons C + D}$ ?

Expliquez pourquoi des graphiques différents peuvent correspondre à une même équation.

Si un graphique ne correspond pas à l'équation donnée, trouvez l'équation chimique qui peut bien s'adapter à ce graphique ?

Détermination des concentrations molaires à l'équilibre

Soit la réaction de dissociation : $\ce{A2_{(g)} \rightleftharpoons 2A_{(g)}}$

On a un système à l'équilibre dont le nombre de moles est donné dans la première ligne du tableau ci-dessous. Calculez le nombre de moles au départ.

Calculez la $K_{\mathrm{c}}$.

En modifiant le volume du récipient, on déplace cet équilibre, et on obtient une nouvelle répartition des moles (cf. deuxième ligne du tableau ci-dessous). En utilisant ces valeurs, calculez $V_2$.

Déplacement de l'équilibre (Principe de Le Châtelier)

Influence de la concentration

Dans la réaction de transformation du sucre $\ce{C6H12O6}$ en éthanol, qu'arrive-t-il si on ajoute du sucre ? Et si on agite la réaction pour éliminer le gaz carbonique ?

Influence de la température

Influence de la pression (par un changement de volume)

Catalyse

Comment agit un catalyseur ?

Soit la réaction $\ce{A + 3B \rightleftharpoons 2C} \quad \Delta H_{\mathrm{r}} = +50\,\mathrm{kJ}$: interprétez chacune des trois situations qui s'éloignent de la situation de référence, définie par les conditions ambiantes :

Exercices SERIE Equilibre chimique

Soit la réaction : $\ce{NH4NO3_{(s)} -> NH4+_{(aq)} + NO3^{-}_{(aq)}} $

Calculez $\Delta H^\circ_{\mathrm{r}} $ and $\Delta S^\circ_{\mathrm{r}} $ de cette réaction.

Calculez $\Delta G^\circ_{\mathrm{r}} $ pour cette réaction à $25\mathrm{^\circ C}$, et expliquez pourquoi $\ce{NH4NO3}$ se dissout spontanément aux conditions ambiantes.

Sans effectuer aucun calcul, dites si l'entropie du système augmente ou diminue au cours du processus et justifiez:

l'oxydation de l'azote: $\ce{N2_{(g)} + 2O2_{(g)} -> 2NO2_{(g)}}$

la sublimation de la glace carbonique: $\ce{CO2_{(s)} -> CO2_{(g)}}$

le refroidissement de l'eau de $50\mathrm{^\circ C}$ à $4\mathrm{^\circ C}$

Calculez la température à partir de laquelle la réduction de l'oxyde de fer ($\ce{III}$) en fer par le carbone, selon la réaction $\ce{2Fe2O3_{(s)} + 3C_{(s)} -> 4Fe_{(s)} + 3CO2_{(g)}}$ devient thermodynamiquement possible.

Donnez l'expression de la constante d'équilibre $K_{\mathrm{c}}$ pour les réactions suivantes :

$\ce{N2O4_{(g)} \rightleftharpoons 2 NO2_{(g)} }$

$\ce{N2_{(g)} + 3 H2_{(g)} \rightleftharpoons 2 NH3_{(g)}}$

Pour la réaction $\ce{SO3_{(g)} \rightleftharpoons SO2_{(g)} + 1/2 O2_{(g)}}$, à $100\mathrm{^\circ C}$, $K_{\mathrm{c}}$ est de $4,07\times 10^{-3}$. Calculez $K_{\mathrm{p}}$ à la même température.

Soit la réaction : $\ce{N2_{(g)} + O2_{(g)} \rightleftharpoons 2 NO_{(g)}} \quad \Delta H^\circ_{\mathrm{r}}>0$ .

$K_{\mathrm{c}}$ à l'équilibre est = $4,8.10^{-3}$ à température ambiante. Que nous dit ce chiffre ?

À température ambiante, y a-t-il beaucoup de $\ce{NO}$ formé ?

Soit la réaction : $\ce{COCl2_{(g)} \rightleftharpoons CO_{(g)} + Cl2_{(g)} }$ $K_{\mathrm{p}}=116$. Calculez $p_{\ce{COCl2}}$ à l'équilibre sachant que $p_{\ce{CO}}$ = $80\,\mathrm{atm}$ et $p_{\ce{Cl2}}$ = $130\,\mathrm{atm}$.

Soit la réaction : $\ce{H2_{(g)} + I2_{(g)} \rightleftharpoons 2 HI_{(g)}}$. On remplit un réacteur de $10$ litres avec $0,5\,\mathrm{mol}$ de $\ce{H2}$ et $0,5\,\mathrm{mol}$ de $\ce{I2}$ à $448\mathrm{^\circ C}$. La constante $K_{\mathrm{c}}$ à cette température est de $50$.

Calculez les molarités ($\,\mathrm{mol/L}$) des gaz à l'équilibre.

Calculez les pressions partielles des gaz à l'équilibre.

Dans la réaction d'estérification : acide acétique + éthanol $\rightleftharpoons$ acétate d'éthyle + eau. À $25\mathrm{^\circ C}$, à l'équilibre, on a : $K_{\mathrm{c}} = 4,1$ , [acide] =$0,21\,\mathrm{mol/L} $, [acetate] = $0,91\,\mathrm{mol/L}$ , [eau] = $0,0085\,\mathrm{mol/L}$.

Calculez la concentration à l'équilibre en éthanol.

Soit la réaction : $\ce{2SO2 + O2 \rightleftharpoons 2 SO3} \qquad \Delta H^\circ_{\mathrm{r}} = - 188\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température faut-il se placer pour déplacer cet équilibre à droite ?

Soit la réaction : $\ce{4NH3 + 5O2\rightleftharpoons 4NO + 6H2O} \qquad \Delta H^\circ_{\mathrm{r}} = - 895\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température faut-il se placer pour déplacer cet équilibre à droite ?

Soit la réaction : $\ce{2CO + O2 \rightleftharpoons 2CO2} \qquad \Delta H^\circ_{\mathrm{r}} = - 568\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température le mélange est plus riche en monoxyde de carbone ?

Soit la réaction : $\ce{N2 + O2\rightleftharpoons 2NO} \qquad \Delta H^\circ_{\mathrm{r}} = +184\,\mathrm{kJ/mol}$. Dans quelles conditions de pression et de température le mélange est plus riche en monoxyde d'azote ?

Soit la réaction : $\ce{2H2O_{g}\rightleftharpoons 2H2 + O2} \qquad \Delta H^\circ_{\mathrm{r}} = +485\,\mathrm{kJ/mol}$. Comment faut-il modifier la pression et la température pour décomposer l'eau selon cette réaction ?

Soit la réaction $\ce{H2 + I2\rightleftharpoons 2HI} \qquad \Delta H^\circ_{\mathrm{r}} = +52\,\mathrm{kJ/mol}$. Comment faut-il modifier la pression et la température pour déplacer cet équilibre vers la droite ?

Soit la réaction s'effectuant dans l'eau: $\ce{As2O3 + 2H2O + 2I2 \rightleftharpoons As2O5 + 4HI}$Dans quel sens est déplacé cet équilibre si l'on ajoute au mélange une solution d'hydroxyde de sodium ?

Calculez la constante d'équilibre $K_{\mathrm{c}}$.

Déterminez le nombre de mole de $\ce{Cl2}$ à l'équilibre lorsqu'une mole de $\ce{PCl5}$ est chauffée à $250\mathrm{^\circ C}$ dans un ballon de $10$ litres.

Même question que la précédante, mais pour un ballon de $1$ litre. Les résultats sont-ils en accord avec le principe de Le Châtelier ?

L'explosion est une réaction de combustion violente:

Quels sont les facteurs qui influencent la vitesse de réaction ?

Qu'est-ce qu' un catalyseur ? Quel est son effet sur une réaction ?

Que deviennent les produits dans une réaction exothermique ? Plus stables ou moins stables que les réactifs de départ ?

Quelle est l'unité de la vitesse de réaction ?

La réaction d'estérification est trop lente si on chauffe ensemble seulement un alcool et un acide carboxylique. Que suggérez-vous pour faire accélérer la réaction ?

Soit la réaction de synthèse de l'ammoniac : $\ce{N2_{(g)} + 3 H2_{(g)} \rightleftharpoons 2 NH3_{(g)}}$ $\Delta H^\circ_{\mathrm{r}} = - 92\,\mathrm{kJ}$. Quel sera l'effet produit sur l'équilibre par :

une augmentation de température ?

Soit la réaction s'effectuant dans l'eau: $\ce{As2O3 + 2H2O + 2I2 \rightleftharpoons As2O5 + 4HI}$
Dans quel sens est déplacé cet équilibre si l'on ajoute au mélange une solution d'hydroxyde de sodium ?