L'eau minérale
Nous discuterons ici les différents équilibres chimiques permettant d'obtenir le $\ce{pH}$ de l'eau minérale. Le lien antre la quantité de $\ce{CO2}$ dans l'air et l'acidification de l'eau sera également présenté.
Le taux de $\ce{CO2}$ dans l'air
Depuis les mesures effectuée en $1870$, le taux de $\ce{CO2}$ a nettement augmenté. Le graphique ci-dessous montre l'évolution de ce taux mesuré à Hawaï1.
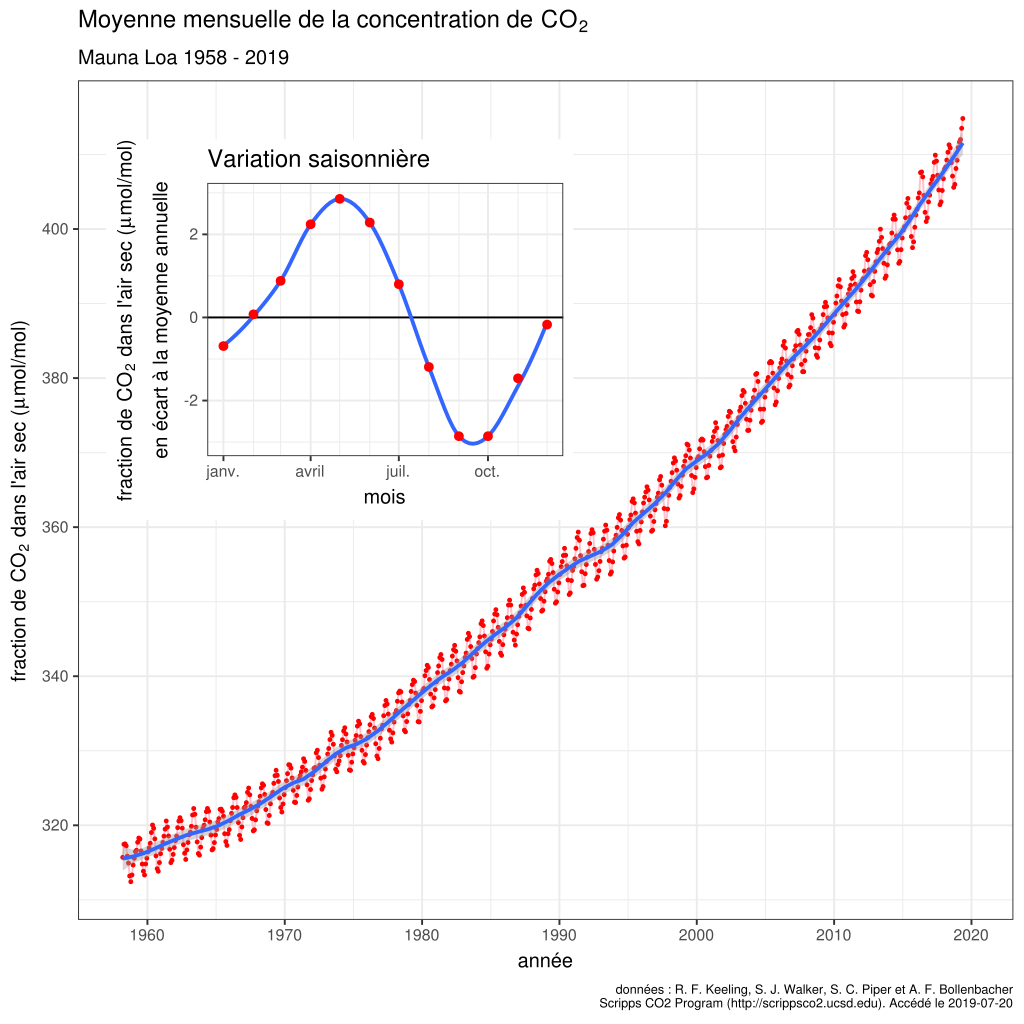
Évolution du taux de $\ce{CO2}$ mesuré dans l'air à l'observatoire de Mauna Loa, à Hawai. L'encart présente les fluctuations saisonnières, dues à la photosynthèse.
La valeur actuelle est d'environ $400\,\mathrm{ppm}$ en volume. L'unité $\mathrm{ppm}$ signifie part par million. Le tableau illustre la proportionnalité existante entre les différentes grandeurs.
| Taux de $\ce{CO2}$ | Volume | Quantité | Pression |
|---|---|---|---|
| $~400\,\mathrm{ppm}$ | $\frac{4\times 10^{-4}\,\mathrm{L}}{1\,\mathrm{L}}\,\frac{\ce{CO2}}{\text{air}}$ | $\frac{4\times 10^{-4}\,\mathrm{mol}}{1\,\mathrm{mol}}\,\frac{\ce{CO2}}{\text{air}}$ | $\frac{4\times 10^{-4}\,\mathrm{atm}}{1\,\mathrm{atm}}\,\frac{\ce{CO2}}{\text{air}}$ |
A partir de la pression partielle exercée par le $\ce{CO2}$, on peut déterminer la molarité du $\ce{CO2}$ à l'aide de la loi des gaz parfaits (à $25\,\mathrm{^\circ C}$): $$ \frac{n}{V}=\frac{p}{R\cdot T}=\frac{4\times 10^{-4}}{0,08206 \cdot298}=1,64\times 10^{-5}\,\mathrm{\frac{mol}{L}} $$ Cette molarité est constante: on fait l'hypothèse que le $\ce{CO2}$ est constamment formé dans l'atmosphère. Si le taux de $\ce{CO2}$ devait continuer à augmenter avec la même vitesse, l'acidité serait excessive pour les organismes vivants dotés de squelette externe (calcifiants).
Les équilibres dans l'eau
L'eau naturelle est considérée comme un système ouvert, dans lequel plusieurs équilibres s'établissent - pensez à l'eau du lac Léman. L'excellente image ci-dessous les résume2 :
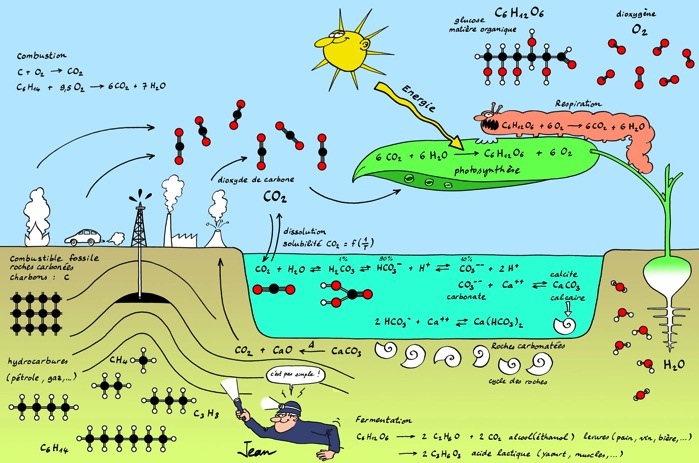
Les équilibres chimiques dans l'eau et dans l'air.
Voici les expressions des constantes pour chaque équilibre:
| Equilibre | Constante | Valeur de la constante |
|---|---|---|
| $\ce{CO2_{(g)}\rightleftharpoons CO2_{(aq)}=\,H2CO3 }$ | $K_\mathrm{c} =\frac{\ce{[CO2_{(g)}]}}{\ce{[H2CO3]}}$ | $K_\mathrm{c} =8,3\times 10^{-1}$ (3) |
| $\ce{H2CO3 +H2O \rightleftharpoons HCO3^{-} + H3O+ }$ | $K_\mathrm{ab} =\frac{\ce{[HCO3^{-}][H3O+]}}{\ce{[H2CO3]}}$ | $K_\mathrm{ab} =4,47\times 10^{-7}$ |
| $\ce{HCO3^{-} +H2O \rightleftharpoons CO3^{2-} + H3O+ }$ | $K_\mathrm{ab} =\frac{\ce{[CO3^{2-}][H3O+]}}{\ce{[HCO3^{-}]}}$ | $K_\mathrm{ab} =5,62\times 10^{-11}$ |
| $\ce{CaCO3_{(s)} \rightleftharpoons Ca^{2+} + CO3^{2-} }$ | $K_\mathrm{s} =\ce{[Ca^{2+}][CO3^{2-}]}$ | $K_\mathrm{s} =5\times 10^{-9}$ |
| $\ce{2H2O \rightleftharpoons H3O+ + OH^{-} }$ | $K_\mathrm{e} =\ce{[H3O+][OH^{-}]}$ | $K_\mathrm{e} =1\times 10^{-14}$ |
Nous avons cinq équations mathématiques, mais six inconnues.
| $\ce{[H2CO3]}$ | $\ce{[HCO3^{-}]}$ | $\ce{[CO3^{2-}]}$ | $\ce{[Ca^{2+}]}$ | $\ce{[H3O+]}$ | $\ce{[OH^-]}$ |
|---|---|---|---|---|---|
| $z$ | $u$ | $s$ | $t$ | $h$ | $w$ |
Il est donc nécessaire d'ajouter une sixième équation. Nous l'avons déjà, car elle est donnée par la neutralité d'une solution: le nombre de charges positives doit être égal au nombre des charges négatives: $$ \ce{[H3O+] + 2[Ca^{2+}]\,=\,[HCO3^{-}] + 2 [CO3^{2-}] + [OH^{-}]} $$ La résolution du système à six équations et six inconnues nous permet de déterminer la molarité en $\ce{H3O+}$ et calculer ainsi le $\ce{pH}$.
L'acidification de l'eau minérale
Comme vu plus haut, le dioxyde de carbone ($\ce{CO2 }$) peut se dissoudre dans l’eau : ceci semblerait un point positif, car la quantité de dioxyde de carbone dans l’atmosphère en résulterait réduite. Cependant, le $\ce{CO2 }$ peut aussi causer l'acidification des océans, diminuant ainsi l’alcalinité (=basicité) de l’eau de mer, processus qui s’accroît avec l’augmentation du niveau de $\ce{CO2 }$ produit par les activités humaines.
Les projections actuelles suggèrent que le $\ce{pH}$ moyen à la surface de l'océan chutera à environ $7,7$ d'ici $2100$, une diminution qui représenterait une augmentation d'environ $150\%$ de l'acidité par rapport au niveau actuel 4.
Pourquoi alors se préoccupe-t-on de l'acidité des océans accrue par le $\ce{CO2 }$ ?
La réponse se trouve dans l'image ci-dessous.

L'acidification de l'eau est susceptible d'impacter toutes les espèces marines mais les organismes calcifiants y sont les plus sensibles.
Exercices
Calculez le $\ce{pH}$ de l'eau minérale.
Quels ont les équilibres présents dans l'eau de pluie ? Que vaut son $\ce{pH}$ ?
Résolution - Calcul du pH de l'eau minérale
Voici le système d'équations: on exprime toutes la inconnues en fonction de la molarite en $\ce{H3O+}\,=\,h\,$:
| $8,3\times 10^{-1}=\frac{10\times 10^{-5}}{z}$ | $z=1,98\times 10^{-5}$ | |
| $4,47\times 10^{-7}=\frac{u\cdot h}{z}$ | $4,47\times 10^{-7}=\frac{u\cdot h}{1,98\times 10^{-5}}$ | $u=\frac{8,83\times 10^{-12}}{h}$ |
| $5,62\times 10^{-11}=\frac{s\cdot h}{u}$ | $5,62\times 10^{-11}=\frac{s\cdot h^2}{8,83\times 10^{-12}}$ | $s=\frac{4,96\times 10^{-22}}{h^2}$ |
| $5\times 10^{-9}=t\cdot s$ | $5\times 10^{-9}=t\cdot \frac{4,96\times 10^{-22}}{h^2}$ | $t = 1,01\times 10^{13}\cdot h^2$ |
| $1\times 10^{-14} = h\cdot w$ | $w=\frac{1\times 10^{-14}}{h}$ |
On reprend l'équation de la neutralité électrique de la solution ($\text{Charges}\,+=\text{Charges}\,-$): $$ \ce{[H3O+] + 2[Ca^{2+}]\,=\,[HCO3^{-}] + 2 [CO3^{2-}] + [OH^{-}]} $$
qui s'écrit: $$ h + 2t = u + 2s + w $$ et qui donne, à partir du développement fait un plus haut, l'équation suivante: $$ h + 2\cdot 1,01\times 10^{13}\cdot h^2 = \frac{8,83\times 10^{-12}}{h} + 2\cdot\frac{4,96\times 10^{-22}}{h^2}+\frac{1\times 10^{-14}}{h} $$
A ce stade, nous ne cherchons pas les solutions analytiques de cette équation ($h= ...$), mais nous procéderons par la méthode graphique qui consiste à tracer les deux courbes $(\text{Charges}\,+\, ; \,\text{Charges}\,-)$ en fonction du $\ce{pH}$ (pour rappel: $\ce{[H3O+]}= h = 10^{-\ce{pH}} $) : $$ \begin{aligned} & \text{Courbe Charges}\, + \qquad = h + 2\cdot 1,01\times 10^{13}\cdot h^2 \\ &\text{Courbe Charges}\,- \qquad = \frac{8,83\times 10^{-12}}{h} + 2\cdot\frac{4,96\times 10^{-22}}{h^2}+\frac{1\times 10^{-14}}{h} \end{aligned} $$
L'interception de ces deux courbes nous donnera la solution pour $h$, et donc pour le $\ce{pH}$.
Nous ferons varier le $\ce{pH}$ entre les valeurs de $7$ et $9$ qui sont plausibles pour un échantillon d'eau minérale (en général, légèrement basique). Nous exclurons ainsi les solutions non plausibles (en dehors des valeurs de $\ce{pH}$ attendues).
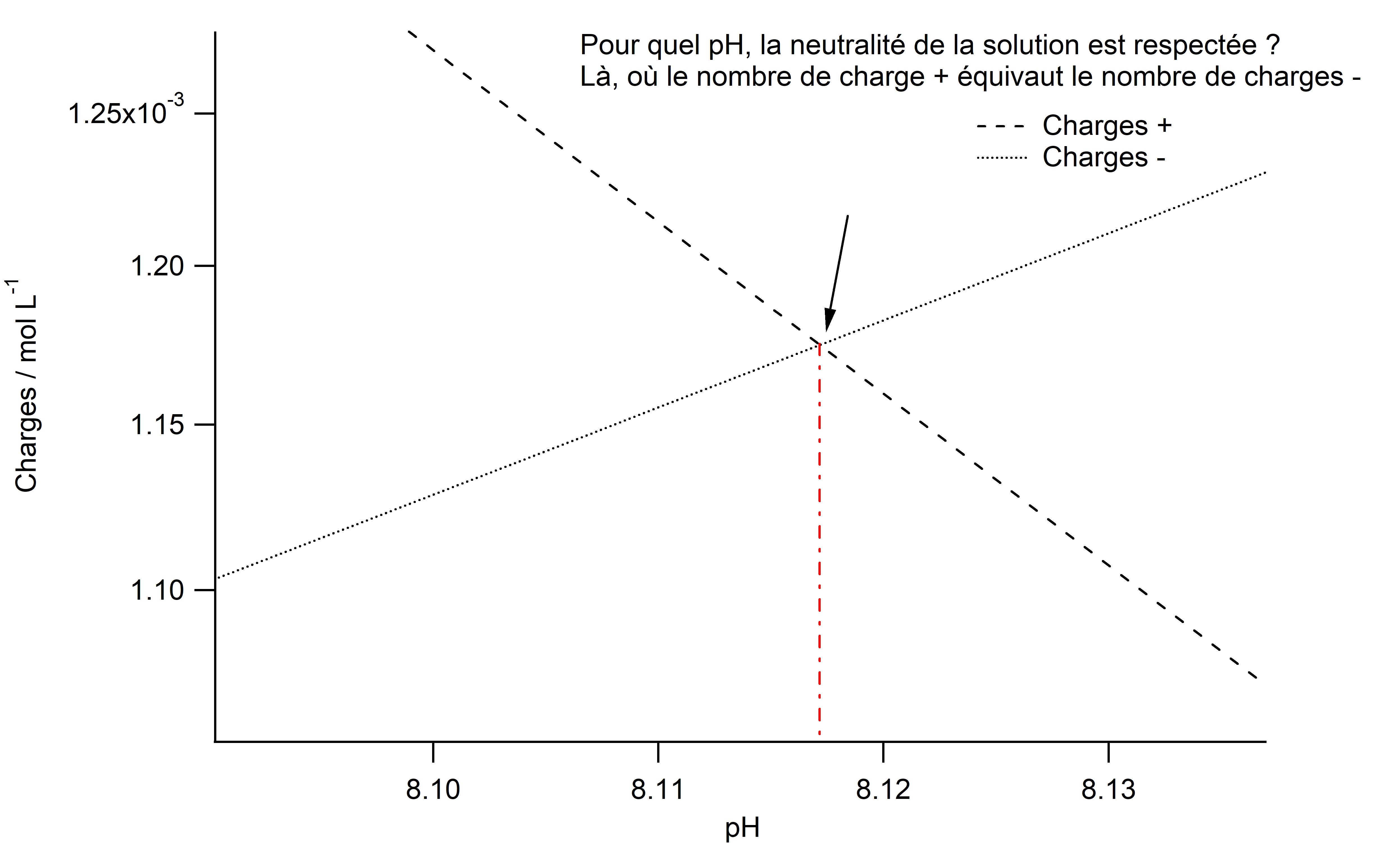
La variation des $\text{Charges}\,+$ et des $\text{Charges}\,-$ en fonction du $\ce{pH}$. L'interception des deux courbes donne le $\ce{pH}$ de l'eau minérale.
Le $\ce{pH}$ de l'eau minérale est donc d'environ $8,12$, pour un taux de $\ce{CO2}$ dans l'air égal à $400\,\mathrm{ppm}$ .
Bibliographie
Voici quelques liens consultés et/ou repris tels quels. Merci à leurs auteurs pour le précieux partage de ces ressources:
-
https://fr.wikipedia.org/wiki/Dioxyde_de_carbone - consulté en mai 2020. ↩
-
http://www.jeanduperrex.ch/Site/Calcaire.html - consulté en mai 2020. ↩
-
https://fr.wikipedia.org/wiki/Loi_de_Henry - consulté en mai 2020. ↩
-
https://www.compoundchem.com/2017/01/18/ocean-acidification-co2/ - consulté en mai 2020 ↩