L'équilibre acide-base
Ce chapitre est consacré aux équilibres acide-base qui ont lieu en solution aqueuse. Nous apprendrons à reconnaitre un acide fort et le différencier d'un acide faible, et on fera de même pour les bases fortes et faibles. Le $\ce{pH}$ sera introduit comme mesure de l'acidité d'une solution. Les issues environnementales, très présentes de nos jours et liées aux variations du $\ce{pH}$, seront également discutées.
Acides et bases
Un acide fort, une base forte ont respectivement une forte tendance à libérer ou à capter un ion $\ce{H+}$. Ils sont totalement dissociés en milieu aqueux. Leur réaction avec l'eau n'aboutit pas à un système à l'équilibre. Exemple :
Un acide faible, une base faible ont respectivement une faible tendance à libérer ou à capter un ion $\ce{H+}$. Ils sont partiellement dissociés en milieu aqueux. Leur réaction avec l'eau aboutit à un système à l'équilibre. Exemple :
Comment une espèce chimique (molécule ou ion) peut posséder un caractère acide ?
- Elle peut avoir un ou des hydrogènes liés directement à un ou des éléments très électronégatifs. Ces liaisons $\ce{H}-$élément doivent être les liaisons les plus polaires de la molécule, ou
- Elle peut être pauvre en électron (ion positif), avec une tendance à capter des électrons.
Exemple : $\ce{HNO3}$, $\ce{CH3COOH}$, $\ce{Na+}$
Comment une espèce chimique (molécule ou un ion) peut posséder un caractère basique ?
-
Elle doit être riche en électron (charge entière ou partielle négative) ou
-
Elle doit posséder au moins une paire d'électron libre.
Exemple: $\ce{KOH}$, $\ce{NH3}$, $\ce{Cl-}$
L'eau pure
L'eau est presque totalement constituée de molécules de $\ce{H2O}$. Celles-ci, appelées ampholytes, peuvent en effet se comporter, soit comme des acides, soit comme des bases, formant ainsi des ions. Seule une molécule sur $555$ millions réagit selon :
$$ \begin{array}{c@{\quad}c} \ce{H2O} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{H3O+} & \ce{+} & \ce{OH^{-}} \\ \text{base} & & \text{acide} & & \text{acide} & & \text{base} \\ \end{array} $$
Écrivons l'expression de la constante d'équilibre (loi d'action de masse ou de Guldberg et Waage) pour cette réaction : $$ K_{\mathrm{c}}=\frac{[\ce{H3O+}]\cdot [\ce{OH-}]}{[\ce{H2O}]} $$
L'eau étant très peu dissociée, sa concentration peut être considérée comme constante : elle est de $55,5\,\mathrm{mol/L}$. Nous pouvons alors écrire:
$$ K_{\mathrm{e}} = [\ce{H3O+}]\cdot [\ce{OH-}]= 10^{-14} $$
$K_{\mathrm{e}}$ est nommé produit ionique de l'eau à $25^\circ C$.
Cette valeur de $10^{-14}$ reste valable pour tout milieu acide ou basique dilué, c'est-à-dire pour des concentrations inférieures à $1\,\mathrm{mol/L}$.
Dans l'eau pure, les concentrations de $\ce{H3O+}$ et $\ce{OH-}$ sont donc égales et elles valent $10^{-7}\,\mathrm{mol/L}$.
Comment peut-on déterminer le nombre de $55,5$ pour la molarité de l'eau dans l'eau ?
Notez que toutes les espèces chimiques traitées dans la suite de ce chapitre sont entendues en milieu aqueux. Pour une question de clarté, l'abréviation (aq) ne sera pas systématiquement indiquée.
Acides forts
Un acide se dit fort lorsqu'il est complétement dissocié dans l'eau. L'équation de protolyse (= réaction chimique dans laquelle un proton est transféré entre deux espèces chimiques) s'écrit comme suit:
$$ \begin{array}{c@{\quad}c} \ce{HCl} & \ce{+} & \ce{H2O} & \ce{->} & \ce{Cl-} & \ce{+} & \ce{H3O+} \\ \text{acide} & & \text{base} & & \text{base} & & \text{acide} \\ \end{array} $$
Vous noterez la flèche unique, de gauche à droite, qui veut indiquer que la dissociation est complète. On peut ainsi affirmer qu'il n'y a pas de molécules d'acide fort indissociées dans l'eau: l'espèce $\ce{HCl_{(aq)}}$ n'existe donc pas. On peut également dire que, si équilibre a lieu, ceci est fortement déplacé à droite.
La base $\ce{Cl-}$ est formellement une base, mais tellement faible d'être incapable d'agir en tant que base. De manière générale, on négligera les bases issues de la dissociation d'un acide fort.
En d'autres termes, l'équilibre ci-dessous est fortement déplacé vers la gauche:
$$
\begin{array}{c@{\quad}c}
\ce{Cl-} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{HCl} & \ce{+} & \ce{OH-} \\
\text{base} & & \text{acide} & & \text{acide} & & \text{base} \\
\end{array}
$$
Nous mettons ici en évidence les deux couples acide/base:
| Couple acide/base | |
|---|---|
| $\ce{HCl / Cl-}$ | $\ce{Cl-}$ est la base conjuguée de $\ce{HCl}$ |
| $\ce{H3O+ / H2O}$ | $\ce{H3O+}$ est l'acide conjugué de $\ce{H2O}$ |
Bases fortes
Une base se dit forte lorsqu'elle est complétement dissociée dans l'eau. L'équation de protolyse s'écrit comme suit:
$$ \begin{array}{c@{\quad}c} \ce{NaOH} & \ce{->} & \ce{Na+} & \ce{+} & \ce{OH-} \\ \text{base} & & \text{acide} & & \text{base} \\ \end{array} $$
Comme pour les acides forts, on peut affirmer qu'il n'y a pas de molécules de bases fortes indissociées dans l'eau: l'espèce $\ce{NaOH_{(aq)}}$ n'existe donc pas. On peut également dire que, si équilibre a lieu, ceci est fortement déplacé à droite.
L'acide $\ce{Na+}$ est formellement un acide, mais tellement faible d'être incapable d'agir en tant qu'acide. De manière générale, on négligera les acides issus de la dissociation d'une base forte.
En d'autres termes, l'équilibre ci-dessous est fortement déplacé vers la gauche:
$$
\begin{array}{c@{\quad}c}
\ce{Na+} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{NaOH} & \ce{+} & \ce{H3O+} \\
\text{acide} & & \text{base} & & \text{base} & & \text{acide} \\
\end{array}
$$
Nous mettons ici en évidence les deux couples acide/base:
| Couple acide/base | |
|---|---|
| $\ce{Na+ / NaOH}$ | $\ce{Na+}$ est l'acide conjugué de $\ce{NaOH}$ |
| $\ce{H2O / OH-}$ | $\ce{OH-}$ est la base conjuguée de $\ce{H2O}$ |
Acides faibles
Si nous ajoutons à l'eau un acide faible comme $\ce{CH3COOH}$, l'eau se comportera comme une base et il s'établira l'équilibre de protolyse suivant :
$$ \begin{array}{c@{\quad}c} \ce{CH3COOH} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{CH3OO-} & \ce{+} & \ce{H3O+} \\ \text{acide} & & \text{base} & & \text{base} & & \text{acide} \\ \end{array} $$
Les deux espèces $\ce{CH3COOH}$ et $\ce{CH3COO-}$ coexistent, mais la forme acide est prédominante. Plus l'acide est faible, plus l'équilibre sera déplacé vers la gauche. Notez que les $\ce{H3O+}$ issus de la protolyse de l'acide vont rendre le $\ce{pH}$ acide.
$\ce{CH3COO-}$ est une base, capable d'agir en tant que telle. En général, la base conjuguée d'un acide faible n'est pas négligeable et peut donc influer sur le $\ce{pH}$ d'une solution.
On peut montrer le comportement basique de $\ce{CH3COO-}$par :
$$
\begin{array}{c@{\quad}c}
\ce{CH3COO-} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{CH3COOH} & \ce{+} & \ce{OH-} \\
\text{base} & & \text{acide} & & \text{acide} & & \text{base} \\
\end{array}
$$
S'agissant d'une base faible, l'équilibre est déplacé vers la gauche ($\ce{CH3COO^{-}}$ est la particule dominante), mais l'action de cette base n'est pas nulle, comme c'était le cas pour la base conjuguée d'un acide fort.
Voici les couples acide/base:
| Couple acide/base | |
|---|---|
| $\ce{CH3COOH / CH3COO-}$ | $\ce{CH3COO-}$ est la base conjuguée de $\ce{CH3COOH}$ |
| $\ce{H3O+ / H2O}$ | $\ce{H3O+}$ est l'acide conjugué de $\ce{H2O}$ |
Si nous appliquons la loi de Guldberg et Waage à l'équilibre eau/acide acétique, la concentration de l'eau pouvant être considérée comme constante, nous avons :
$$ K_\mathrm c=K_\mathrm {ab}=\frac{[\ce{CH3COO-}]\cdot [\ce{H3O+}]}{[\ce{CH3COOH}]} $$
Notez que nous utilisons l'abréviation $K_\mathrm {ab}$ pour indiquer la constante d'un équilibre acide base. Il sera très pratique de calculer le $log$ négatif de la constante, pour obtenir le $\mathrm pK_\mathrm {ab}$ . $$ \mathrm pK_\mathrm {ab}=-log(K_\mathrm {ab}) $$
On en déduit que:
- plus l'acide est faible, plus la constante $K_\mathrm {ab}$ sera petite et plus le $\mathrm pK_\mathrm {ab}$ sera grand
- plus l'acide est fort, plus la constante $K_\mathrm {ab}$ sera grande et plus le $\mathrm pK_\mathrm {ab}$ sera petit.
Bases faibles
Une base faible comme l'ammoniac, $\ce{NH3}$, interagit avec l'eau qui, elle, se comporte comme un acide. S'établit ainsi l'équilibre de protolyse suivant :
$$ \begin{array}{c@{\quad}c} \ce{NH3} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{NH4+} & \ce{+} & \ce{OH-} \\ \text{base} & & \text{acide} & & \text{acide} & & \text{base} \\ \end{array} $$
Les deux espèces $\ce{NH3}$ et $\ce{NH4+}$ coexistent, mais la forme basique est prédominante. Plus la base est faible, plus l'équilibre sera déplacé vers la gauche. Notez que les $\ce{OH-}$ issus de la protolyse de la base vont rendre le $\ce{pH}$ basique.
$\ce{NH4+}$ est un acide, capable d'agir en tant que tel. En général, l'acide conjugué d'une base faible n'est pas négligeable et peut donc influer sur le $\ce{pH}$ d'une solution.
On peut montrer le comportement acide de $\ce{NH4+}$ par :
$$
\begin{array}{c@{\quad}c}
\ce{NH4+} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{NH3} & \ce{+} & \ce{H3O+} \\
\text{acide} & & \text{base} & & \text{base} & & \text{acide} \\
\end{array}
$$
S'agissant d'un acide faible, l'équilibre est déplacé vers la gauche ($\ce{NH4^{+}}$ est la particule dominante), mais l'action de cet acide n'est pas nulle, comme c'était le case de l'acide conjugué d'une base forte.
Voici les couples acide/base:
| Couple acide/base | |
|---|---|
| $\ce{NH4+ / NH3}$ | $\ce{NH4+}$ est l'acide conjugué de $\ce{NH3}$ |
| $\ce{H2O / OH-}$ | $\ce{OH-}$ est la base conjuguée de $\ce{H2O}$ |
Si nous appliquons la loi de Guldberg et Waage à l'équilibre eau/ammoniac, la concentration de l'eau pouvant être considérée comme constante, nous avons :
$$ K_\mathrm c=K_\mathrm {ba}=\frac{[\ce{NH4+}]\cdot [\ce{OH-}]}{[\ce{NH3}]} $$
Notez que nous utilisons l'abréviation $K_\mathrm {ba}$ pour indiquer la constante d'un équilibre base acide. Toutefois, aussi pour les bases, on préfère utiliser la $K_\mathrm{ab}$. Voici la relation qui existe entre $K_\mathrm {ba}$ et $K_\mathrm{ab}$:
$$ K_\mathrm {ba}=\frac{[\ce{NH4+}]\cdot [\ce{OH-}]}{[\ce{NH3}]}= \frac{[\ce{NH4+}]\cdot [K_\mathrm{e}]}{[\ce{NH3}]\cdot [\ce{H3O+}]}=\frac{K_\mathrm{e}}{K_\mathrm{ab}}=\frac{10^{-14}}{K_\mathrm{ab}} $$
On en déduit que:
- plus la base est faible, plus la constante $K_\mathrm {ab}$ sera grande et plus le $\mathrm pK_\mathrm {ab}$ sera petit
- plus la base est forte, plus la constante $K_\mathrm {ab}$ sera petite et plus le $\mathrm pK_\mathrm {ab}$ sera grand.
Sels
Les sels dissouts dans l'eau sont aussi complétement dissociés. L'équation décrivant cette dissociation est: $$ \ce{MX_{(s)} \rightleftharpoons MX_{(aq)}->M+ + X-} $$ Cette équation signifie que tout particule de sel mélangée à l'eau sera aussi dissociée. Dans ce paragraphe, nous nous focaliserons uniquement sur les sels très solubles, alors qu'un chapitre à part sera dédié aux sels (et hydroxydes) peu solubles. Nous traiterons les situations suivantes:
Sel d'un acide fort et base forte
L'exemple le plus célèbre est le $\ce{NaCl}$, qui origine du $\ce{NaOH}$ et $\ce{HCl}$. Les deux étant forts, leurs espèces conjuguées n'auront aucun effet sur le $\ce{pH}$.
On en déduit que le $\ce{pH}$ sera celui de l'eau pure: donc égal à $7$.
Sel d'un acide faible et base forte
Prenons le cas du $\ce{NaCH3COO}$, qui origine du $\ce{NaOH}$ et $\ce{CH3COOH}$. $$ \ce{NaCH3COO_{(aq)}->Na+ + CH3COO-} $$
Le $\ce{Na+}$ est un acide négligeable (car conjugué d'une base forte). La base $\ce{CH3COO-}$ doit être prise en compte, car cet équilibre s'établit dans l'eau:
$$ \begin{array}{c@{\quad}c} \ce{CH3COO-} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{CH3COOH} & \ce{+} & \ce{OH-} \end{array} $$
On utilisera la formule du $\ce{pH}$ d'une base faible, pour calculer le $\ce{pH}$ de la solution saline.
Sel d'un acide fort et base faible
Prenons le cas du $\ce{NH4Cl}$, qui origine de $\ce{NH3}$ et $\ce{HCl}$. $$ \ce{NH4Cl_{(aq)}->NH4+ + Cl-} $$
Le $\ce{Cl-}$ est une base négligeable (car conjuguée d'un acide fort). L'acide $\ce{NH4+}$ doit être pris en compte, car cet équilibre s'établit dans l'eau:
$$ \begin{array}{c@{\quad}c}\ce{NH4+} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{NH3} & \ce{+} & \ce{H3O+}\end{array} $$
On utilisera la formule du $\ce{pH}$ d'un acide faible, pour calculer le $\ce{pH}$ de la solution saline.
Le $\ce{pH}$
L'échelle de $\ce{pH}$.
Le $\ce{pH}$ est une mesure de l'acidité d'une solution. C'est donc une fonction de la concentration en ions $\ce{H3O+}$ = $\ce{[ H3O+ ]}$. De même, on peut définir le $\ce{pOH}$ comme une fonction de la concentration en ions $\ce{OH-}$. Le $\ce{pH}$ est souvent employé dans la vie courante : le logarithme permet d’éliminer la puissance de $10$ et d’obtenir un chiffre plus facile à retenir.
| Milieu acide | Milieu basique |
|---|---|
| les ions $\ce{H3O+}$ sont dominants | les ions $\ce{OH-}$ sont dominants |
| $\ce{pH}=-log(\ce{[H3O+ ]})$ | $\ce{pOH}=-log(\ce{[OH- ]})$ |
Conversion: du $\ce{pOH}$ au $\ce{pH}$
On utilise rarement le $\ce{pOH}$.
Comment passer alors du $\ce{pOH}$ au $\ce{pH}$ ?
$$
\ce{pH}=14 - \ce{pOH}
$$
Conversion: du $\ce{pH}$ à $\ce{[H3O+]}$
Comment passer du $\ce{pH}$ à la concentration en $\ce{H3O+}$ ?
$$ \ce{[H3O+ ]}=10^{-\ce{pH}} $$
Conversion: de $\ce{[H3O+ ]}$ à $\ce{[OH- ]}$
Comment passer de la concentration en $\ce{H3O+}$ à la concentration en $\ce{OH-}$ (grâce au produit ionique de l'eau $K_\mathrm {e}=10^{-14}$) ? $$ \ce{[OH- ]}=\frac{10^{-14}}{\ce{[H3O+ ]}} $$
Notez que ces formules sont données dans les Tables CRM
(index analytique : chercher le mot « $\ce{pH}$ » ).
L'acidification des océans
Le dioxyde de carbone ($\ce{CO2 }$) peut se dissoudre dans l’eau de mer: ceci semblerait un point positif, car la quantité de dioxyde de carbone dans l’atmosphère en résulterait réduite. Cependant, le $\ce{CO2 }$ peut aussi causer l'acidification des océans, diminuant ainsi l’alcalinité (=basicité) de l’eau de mer, processus qui s’accroît avec l’augmentation du niveau de $\ce{CO2 }$ produit par les activités humaines.
Les projections actuelles suggèrent que le $\ce{pH}$ moyen à la surface de l'océan chutera à environ $7,7$ d'ici $2100$, une diminution qui représenterait une augmentation d'environ $150\%$ de l'acidité par rapport au niveau actuel 1.
Pourquoi alors se préoccupe-t-on de l'acidité des océans accrue par le $\ce{CO2 }$ ?
La réponse se trouve dans l'image ci-dessous.

L'acidification des océans est susceptible d'impacter toutes les espèces marines mais les organismes calcifiants y sont les plus sensibles.
Exercice:
Dans le site1, on affirme qu'une diminution de $0,1$ unités de $\ce{pH}$ représente une augmentation de l'acidité de $25\%$. Comment peut-on le prouver ?
L'échelle de $\ce{pH}$
L'image ci-dessous est tirée de l'excellente collection d'infographies créées par Andy Brunning 2. Notez que les $\ce{pH}$ négatifs comme les $\ce{pH}$ supérieurs à $14$ sont possibles et présents en nature. On citera, par exemple, certaines sources d'eau proches de volcans qui ont un $\ce{pH}$ mesuré inférieur à $0$.
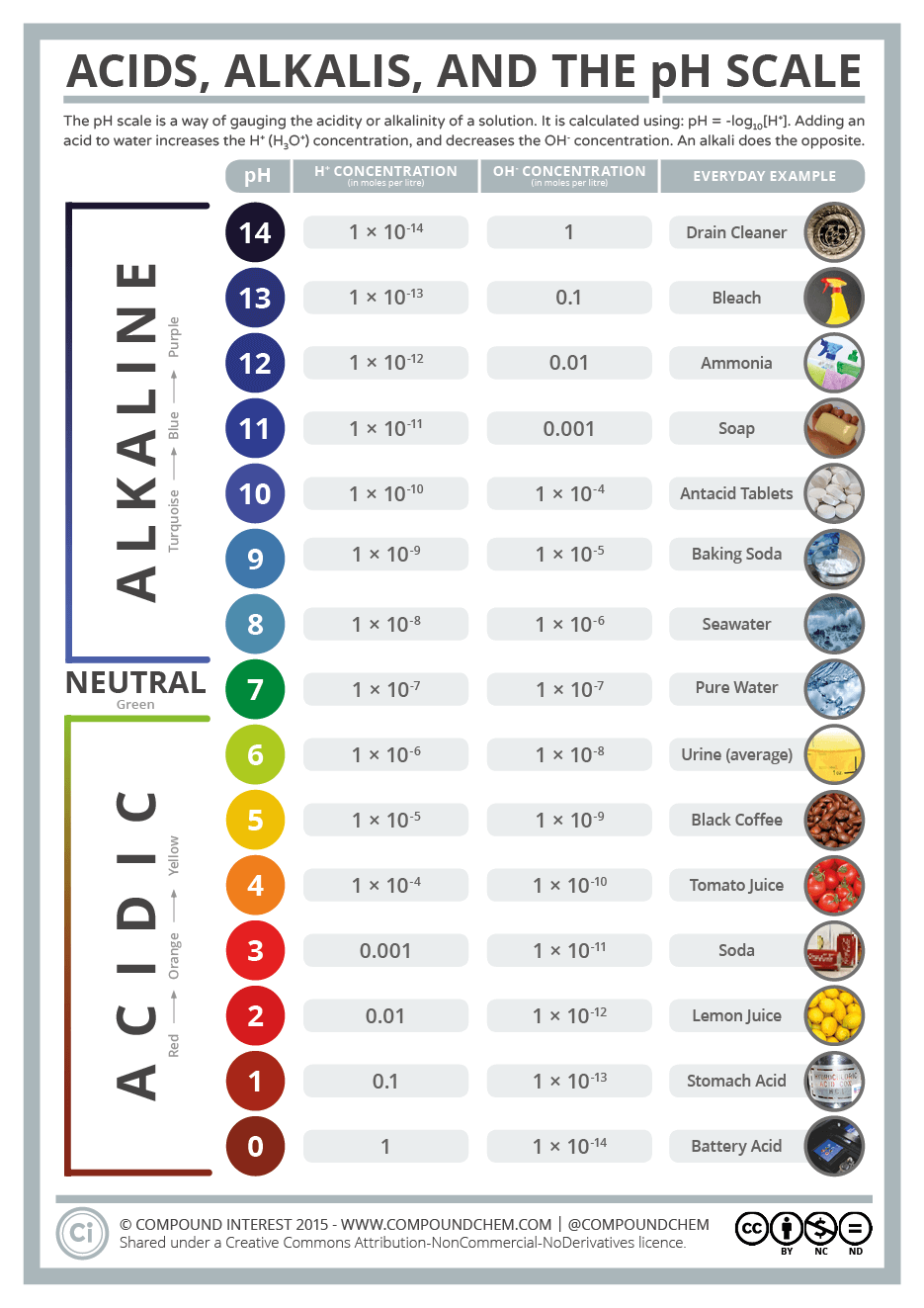
Echelle de pH et produits courants.
Calcul du pH
Nous verrons ici comment s'effectue le calcul du $\ce{pH}$ pour les différentes situations décrites dans ce chapitre.
$\ce{pH}$ des acides forts
Un acide fort est totalement dissocié dans l'eau. Pour $\ce{[HCl]}$, $\ce{[H3O+]=[HCl]}$ et donc $$ \ce{pH}=-log(\ce{[HCl]})=-log(C_a) $$
où $C_a$ est la molarité de l'acide.
$\ce{pH}$ des bases fortes
Une base forte est totalement dissociée dans l'eau. Pour $\ce{[NaOH]}$, $\ce{[OH-]=[NaOH]}$ et donc
$$ \ce{pOH} = -log(\ce{[NaOH]}) = -log(C_b) \\ \ce{pH} = 14 - \ce{pOH} $$ où $C_b$ est la molarité de la base.
$\ce{pH}$ des acides faibles
Un acide faible n'est pas complétement dissocié et est en équilibre avec sa base conjuguée. Nous utiliserons l'expression de la constante $K_\mathrm{ab}$ de l'équilibre acide-base. Prenons le cas d'une solution de $\ce{CH3COOH}$ de molarité initiale $C_a$ et considérons que l'acide est peu dissocié, ce qui nous permet d'approximer la valeur de $\ce{[CH3COOH]}$ à l'équilibre, à la molarité initiale de l'acide:
| Calcul de $[\ce{H3O+}]$ | logarithme négatif | Calcul du $\ce{pH}$ |
|---|---|---|
| $K_\mathrm {ab}=\frac{[\ce{CH3COO-}]\cdot [\ce{H3O+}]}{C_a}=\frac{[\ce{H3O+}]^2}{C_a}$ $\Rightarrow [\ce{H3O+}]=\sqrt{C_a\cdot K_\mathrm {ab} }$ |
$-log([\ce{H3O+}])=-\frac{1}{2}log({C_a\cdot K_\mathrm {ab}) }$ | $\ce{pH}=\frac{1}{2}(pK_\mathrm {ab}-log(C_a) )$ |
L'expression à droite nous permet de calculer le $\ce{pH}$ d'une solution d'acide faible: notez que le $pK_\mathrm {ab}$ apparait dans cette formule.
$\ce{pH}$ des bases faibles
Une acide faible n'est pas complétement dissociée et est en équilibre avec son acide conjugué. Comme pour les acides, nous utiliserons l'expression de la constante $K_\mathrm{ab}$ de l'équilibre acide-base. Prenons le cas d'une solution de $\ce{NH3}$ de molarité initiale $C_b$ et considérons que la base est peu dissociée, ce qui nous permet d'approximer la valeur de $\ce{[NH3]}$ à l'équilibre, à la molarité initiale de la base:
| Calcul de $[\ce{H3O+}]$ | logarithme négatif | Calcul du $\ce{pH}$ |
|---|---|---|
| $K_\mathrm {ab}=\frac{C_b\cdot [\ce{H3O+}]}{[\ce{NH4+}]}=\frac{C_b\cdot [\ce{H3O+}]}{[\ce{OH-}]}=\frac{C_b\cdot [\ce{H3O+}]^2}{K_\mathrm {e}}$ $\Rightarrow [\ce{H3O+}]=\sqrt{\frac{K_\mathrm {e}\cdot K_\mathrm {ab}}{C_b} }$ |
$-log([\ce{H3O+}])=$ $=-\frac{1}{2}log\left(\frac{10^{-14}\cdot K_\mathrm {ab}}{C_b}\right) $ |
$\ce{pH}=\frac{1}{2}(14+pK_\mathrm {ab}+log(C_b) ) $ |
L'expression à droite nous permet de calculer le $\ce{pH}$ d'une solution de base faible: notez ici aussi que le $pK_\mathrm {ab}$ apparait dans cette formule.
$\ce{pH}$ des solution tampons
Une solution tampon est le mélange d'un acide faible et de sa base conjuguée (ou vice-versa). Notez bien qu'il s'agira de mélanger deux espèces, l'une acide et l'autre basique et conjuguée de la première (ou vice-versa), respectivement de molarité $C_a$ et $C_b$. Prenons le cas d'une solution de $\ce{CH3COOH}$ et de $\ce{CH3COO-}$ (provenant d'un sel, comme $\ce{NaCH3COO}$ ).
| Calcul de $[\ce{H3O+}]$ | logarithme négatif | Calcul du $\ce{pH}$ |
|---|---|---|
| $K_\mathrm {ab}=\frac{[C_b]\cdot [\ce{H3O+}]}{C_a}$ $\Rightarrow [\ce{H3O+}]=\frac{C_a}{C_b}\cdot K_\mathrm{ab} $ |
$-log([\ce{H3O+}])=-log\left(\frac{C_a}{C_b}\cdot K_\mathrm {ab}\right) $ | $\ce{pH}=pK_\mathrm {ab}-log\left(\frac{C_a}{C_b} \right)$ |
Pourquoi ce terme, tampon ? Ce type de solution exerce l'effet nommé tampon, c'est à dire un pouvoir de subir des additions d'acide ou de base, sans une grande variation du $\ce{pH}$. Ce pouvoir est efficace à condition que les concentrations des espèces constituant le tampon soient bien plus grandes que celles des ajouts prévus.
Comment préparer une solution tampon ?
- On choisit un couple acide/base dont le $pK_\mathrm {ab}$ est proche du $\ce{pH}$ désiré
- On peut:
- dissoudre dans l'eau l'acide faible et de sa base conjuguée
- ou neutraliser partiellement l'acide faible à l'aide d'une base forte
$\ce{pH}$ des ampholytes
Un ampholyte est une espèce chimique qui est à la fois acide et basique. On peut aussi utiliser l'adjectif amphotère pour décrire ce double caractère.
Un exemple d'ampholyte est l'hydrogénocarbonate de sodium , $\ce{NaHCO3}$, qui se dissocie en $\ce{Na+}$ et $\ce{HCO3-}$. Les deux équilibres attestant le comportement amphotère de $\ce{HCO3-}$ sont:
$$ \begin{array}{c@{\quad}c}\ce{HCO3-} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{CO3^{2-}} & \ce{+} & \ce{H3O+} & \quad K_\mathrm{ab1}=4,47\times 10^{-7} \\ \ce{HCO3-} & \ce{+} & \ce{H2O} & \ce{\rightleftharpoons} & \ce{H2CO3} & \ce{+} & \ce{OH-} & \quad K_\mathrm{ab2}=5,62\times 10^{-11} \end{array} $$
Considérons une solution de $\ce{NaHCO3}$ de molarité égale à $C_s$ . Voici les équations que nous avons à disposition:
| Equation | |
|---|---|
| $1)$ équilibre acide-base 1 | $K_\mathrm {ab1}=\frac{[\ce{CO3^{2-}}]\cdot [\ce{H3O+}]}{[\ce{HCO3-}]}$ |
| $2)$ équilibre acide-base 2 | $K_\mathrm {ab2}=\frac{[\ce{HCO3^{-}}]\cdot [\ce{H3O+}]}{[\ce{H2CO3}]}$ |
| $3)$ Conservation de la masse | $C_s=\ce{[Na+]}=\ce{[H2CO3] + [HCO3^{-}] +[CO3^{2-}]}$ |
| $4)$ Electroneutralité de la solution | $\ce{[Na+] +[H3O+]= [HCO3^{-}] +2[CO3^{2-}] + [OH^{-}]}$ |
En reportant $\ce{[Na+]}$ issu de l'équation $3)$ dans l'équation $4)$, nous obtenons: $$ \ce{[H2CO3] + [H3O+] = [CO3^{2-}] + [OH^{-}]} $$ En faisant hypothèse que la solution soit proche de la neutralité, on peut écrire $\ce{[H2CO3]}\gg\ce{[H3O+]}$ et $\ce{[CO3^{2-}]}\gg\ce{[OH^{-}]}$, l'on obtient $\ce{[H2CO3]}\approx\ce{[CO3^{2-}]}$.
En multipliant l'équation $1)$ et la $2)$ et appliquant l'hypothèse ci-dessus, l'équation suivante s'écrit:
$$
K_\mathrm {ab1}\cdot K_\mathrm {ab2}=\ce{[H3O+]^2}\Rightarrow \ce{[H3O+]}=\sqrt{K_\mathrm{ab1}\cdot K_\mathrm{ab2}}
$$
On termine par écrire la forme logarithmique:
$$
\ce{pH}=\frac{1}{2}\left(pK_\mathrm {ab1}+pK_\mathrm {ab2}\right)
$$
ce qui donne $8,3$ pour le $\ce{NaHCO3}$. Nous constatons que, pour un ampholyte, cette équation approximée ne contient pas la molarité de la solution.
Cette équation n'est valable que:
- pour des molarité assez élevées (supérieures à $0,01\,\mathrm{M}$),
- pour des moyennes arithmétiques entre $pK_\mathrm {ab1}$ et $pK_\mathrm {ab2}$ proches de $7$.
Exercices SERIE $\ce{pH}$
Donner l’acide conjugué de : $\ce{NH3}$, $\ce{NO3-}$, $\ce{HSO4-}$
Donner la base conjuguée de : $\ce{H2S}$, $\ce{HSO4-}$
Si $\ce{[H3O+]}$ = $10^{-2}\, \mathrm{M}$, que vaut $\ce{[OH-]}$ ?
Calculer le $\ce{pH}$ pour $\ce{[H3O+]}$ = $10^{-1}\, \mathrm{M}$, pour $\ce{[H3O+]}$ = $0,001\, \mathrm{M}$ et pour $\ce{[H3O+]}$ = $3,6\times 10^{-3}\, \mathrm{M}$.
Calculer $\ce{[H3O+]}$ pour $\ce{pH} =3$, pour $\ce{pH} =5$ et pour $\ce{pH} =8,5$.
Que vaut le $\ce{pH}$ d’une solution de $\ce{HCl}$ $0,025\,\mathrm{mol/L}$ ?
Que vaut le $\ce{pH}$ d’une solution de $\ce{NaOH}$ $0,0025\,\mathrm{mol/L}$ ?
Que devient le $\ce{pH}$ si on ajoute $90\,\mathrm{mL}$ d'eau à $10\,\mathrm{mL}$ d'une solution acide dont le $\ce{pH}$ est $0,3$ ?
Que devient le $\ce{pH}$ d'une solution de $\ce{HCl}$ dont le $\ce{pH}$ est $2$ si on la dilue $10$ fois (= le volume devient $10$ fois plus grand)?
Quel est le $\ce{pH}$ d'un mélange de $100\,\mathrm{mL}$ de $\ce{H2SO4}$ $0,1\,\mathrm{mol/L}$ avec $300\,\mathrm{mL}$
de $\ce{HCl}$ $0,3\,\mathrm{mol/L}$ ?
Quel est le $\ce{pH}$ d'un mélange de $100\,\mathrm{mL}$ de $\ce{H2SO4}$ $0,1\,\mathrm{mol/L}$ avec $200\,\mathrm{mL}$ de $\ce{NaOH}$ $0,1\,\mathrm{mol/L}$ ?
Quel est le $\ce{pH}$ d'un mélange de $100\,\mathrm{mL}$ de $\ce{H2SO4}$ $0,1\,\mathrm{mol/L}$ avec $200\,\mathrm{mL}$ de $\ce{NaOH}$ $0,2\,\mathrm{mol/L}$ ?
On dissout de l'acide fluorhydrique dans de l'eau. Écrivez la réaction de protolyse. Que faut-il ajouter à cette solution pour en diminuer l'acidité ?
Que se passe-t-il si l'on ajoute de l'acide chlorhydrique à une solution de carbonate de
sodium ?
Entre l'acide cyanhydrique et l'acide formique, lequel est l'acide qui se dissocie le plus dans l'eau ? Justifier.
Citer un acide plus fort que l'acide acétique et un acide plus faible que l'acide acétique.
Expliquer pourquoi l'acide carbonique a deux valeurs de $pK_\mathrm {ab}$.
Le pourcentage d'ionisation de l'acide formique $1\,\mathrm{mol/L}$ est de $1,3 %$ à $25^\circ C$. Calculez son $pK_\mathrm {ab}$
Ecrivez la réaction de protolyse de l'acide nitreux. Comment se déplacera l'équilibre :
si l'on ajoute du nitrite de sodium.
si l'on ajoute du $\ce{NaOH}$.
Quel est le $\ce{pH}$ d'une solution d'acide iodhydrique dont le titre est de $2,56\times 10^{-4}\,\mathrm{g/mL}$
Quel est le titre d'une solution de $\ce{HCl}$ de $\ce{pH}=2,3$ ?
Quel est le $\ce{pH}$ d'une solution contenant $0,26\,g$ de $\ce{Ca(OH)2}$ dans $150\,\mathrm{mL}$ de solution ? On fait l'hypothèse que l'hydroxyde est complètement dissocié.
On ajoute $200\,\mathrm{mL}$ d'eau à $200\,\mathrm{mL}$ d'une solution de $\ce{NaOH}$ de $\ce{pH}= 11$. Que devient le $\ce{pH}$ ?
On mélange $600\,\mathrm{mL}$ de $\ce{HCl}$ $0,1\,\mathrm{mol/L}$ avec $700\,\mathrm{mL}$ de $\ce{NaOH}$ $0,2\,\mathrm{mol/L}$. Quel est le $\ce{pH}$ de la solution après le mélange ?
Quel est le $\ce{pH}$ d'une solution de $\ce{NaCN}\,$ $0,1\,\mathrm{mol/L}$ ?
Calculer le $\ce{pH}$ d’une solution contenant $0,05$ d’acide formique dans $500\,\mathrm{mL}$ d’eau.
Quel est le $\ce{pH}$ d'une solution d'acide nitreux dont le titre est de $2,35\,\mathrm{g/L}$ ?
On presse un citron pesant $130\,g$ et on retire $50\,\mathrm{mL}$ de jus de $\ce{pH}=2,5$. Calculez la masse d'acide citrique contenue dans le citron.
Sachant que le piment rouge contient $0,05\, \%$ de vitamine C (acide ascorbique $\ce{C6H8O6}$), calculez le $\ce{pH}$ d'une solution de $2$ litres qui aurait extrait toute la vitamine C de $1,5\,\mathrm{kg}$ de piment rouge. La vitamine C a un $pK_\mathrm {ab}$ de $4,17$ et une masse moléculaire de $176\,\mathrm{u}$.
Donnez un exemple de sel pour chacun des cas suivants :
Sel obtenu à partir d’un acide fort et d’une base forte.
Sel obtenu à partir d’un acide faible et d’une base forte.
Sel obtenu à partir d’un acide fort et d’une base faible.
Les sels suivants sont-ils acides, neutres ou basiques ? Justifiez dans chaque cas brièvement votre réponse.
$\ce{KCl ->}$
$\ce{NH4Cl ->}$
$\ce{NaClO4 ->}$
$\ce{NaNO2 ->}$
$\ce{KNO3 ->}$
Quel est le titre d'une solution d'hypochlorite de sodium de $\ce{pH}=9,2$ ?
Quel est le $\ce{pH}$ d'une solution contenant $0,01\,\mathrm{mol/L}$ de fluorure de sodium et $0,02\,\mathrm{mol/L}$ d'acide fluorhydrique ?
Une solution de $500\,\mathrm{mL}$ contient $1,05\,\mathrm{g}$ de $\ce{HClO}$. Quel en est le $\ce{pH}$ ? Quelle masse de $\ce{NaClO}$ faut-il y ajouter pour obtenir un mélange tampon de $\ce{pH = 7}$ ?
On ajoute $50\,\mathrm{mL}$ de benzoate de sodium $\ce{C6H5COONa}$ $0,01\,\mathrm{mol/L}$ à $25\,\mathrm{mL}$ d'acide benzoïque $0,02\,\mathrm{mol/L}$. Le $\ce{pH}$ du mélange est de $4,2$. Calculez le $pK_\mathrm {ab}$.
On mélange $100\,\mathrm{mL}$ d'une solution de $\ce{NaOH}$ $0,04\,\mathrm{mol/L}$ à $100\,\mathrm{mL}$ d'une solution de $\ce{CH3COOH}$ $0,05\,\mathrm{mol/L}$. Calculez le $\ce{pH}$ du mélange.
Calculez le $\ce{pH}$ d'une solution d'hydrogénosulfite de sodium à $0,23\,\mathrm{mol/L}$ ($pK_\mathrm {ab1} = 1,8$ et $pK_\mathrm {ab2} = 7,2$).
On a besoin d'un litre d'une solution tampon de $\ce{pH} = 10$. Comment doit-on procéder ?
La concentration en acide carbonique dans le sang est de $1,25\times 10^{-3}\,\mathrm{mol/L}$. Le $\ce{pH}$ du sang est de $7,4$. Calculez la concentration en hydrogénocarbonate dans le sang.
Comment préparer $500\,\mathrm{mL}$ de solution tampon de $\ce{pH} = 3,5$ à partir de deux solutions ; une d’$\ce{HNO2}$ $0,025\,\mathrm{mol/L}$ et une seconde de $\ce{NaNO2}$ de $0,045\,\mathrm{mol/L}$ ?
Bibliographie
Voici quelques liens consultés et/ou repris tels quels. Merci à leurs auteurs pour le précieux partage de ces ressources: