Courbes acide-base
Les titrages (ou dosages) acide-base sont une des techniques les plus utilisées en chimie analytique. La méthode consiste à déterminer la quantité d’acide dans une solution en y ajoutant une quantité équivalente d’une base, ou vice-versa. Nous apprendrons à interpréter une courbe acide/base (appelée aussi courbe de neutralisation ou courbe $\ce{pH}$-métrique). Les points d'une courbe acide/base sont le résultat d'un équilibre acide/base qui s'établit en solution. Nous verrons à l'aide de courbes acide/base comment déterminer la concentration de la solution initiale, ainsi que le type d'acide ou de base titré.
Courbe de neutralisation d'un acide fort par une base forte
Appareillage :
- la burette contient la solution titrante de concentration connue
- le bécher récepteur contient la solution à titrer de concentration inconnue et un indicateur coloré acide/base
- l'électrode plongée dans la solution est connectée au $\ce{pH}$-mètre.

L'expérience: comment obtenir une courbe acide/base
Graphique

Un exemple de courbe acide/base.
Détermination au laboratoire du point équivalent
Marche à suivre pour déterminer le volume au point équivalent :
- Tracez les 2 tangentes parallèles à la courbe.
- Tracez la droite perpendiculaire aux tangentes parallèles: le point équivalent est à l'intersection de cette droite et de la courbe pH-métrique.
- Déterminez le volume au point équivalent à la verticale de ce point.
Méthode des tangentes appliquée à une courbe acide/base.
Courbe de neutralisation d'un acide fort par une base forte
Soit la neutralisation de $\ce{HCl}$ par $\ce{NaOH}$ : $\ce{HCl + NaOH → NaCl + H2O}$.
Le volume initial de solution acide est de $10\,\mathrm{mL}$ et la molarité de la solution titrante de $\ce{NaOH}$ est de $0,1\,\mathrm{M}$.

Courbe de neutralisation d'un acide fort par une base forte.
Point d'équivalence
La quantité de titrant ($\ce{NaOH}$) ajouté est égale à la quantité initiale d'acide: on peut écrire que $\ce{mol_{i}} = \ce{mol_{NaOH}}$.
Le volume correspondant au point d'équivalence est égal à $7,5\,\mathrm{mL}$. Cela correspond à $7,5\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=7,5\times 10^{-4}\,\mathrm{mol}$ de $\ce{NaOH}$ . S'agissant du point d'équivalence, ce nombre donne également le nombre de moles initiales d'acide. Nous pouvons ainsi calculer la molarité initiale de la solution acide, comme suit: $\frac{7,5\times 10^{-4}\,\mathrm{mol}}{1\times 10^{-2}\,\mathrm{L}}=0,075\,\mathrm{\frac{mol}{L}}$.
On étudie la variation provoquée par cette addition de $\ce{NaOH}$.
| $\qquad\ce{HCl}$ | $\qquad+$ | $\qquad\ce{NaOH}$ | $\qquad\ce{->}$ | $\qquad\ce{NaCl}$ | $\qquad+$ | $\qquad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\qquad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\qquad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes
$$ \ce{H2O} $$
$\ce{pH}$ au point d'équivalence
$\ce{pH}=7$. La seule particule avec un effet sur le $\ce{pH}$ est la molécule d'eau.
Point initial
Le $\ce{pH}$ avant d'ajouter de la base ($V_{\ce{NaOH}} = 0\,\mathrm{mL}$) est égal au $\ce{pH}$ de la solution acide (acide fort).
Particules dominantes
$$ \ce{H3O+} $$
$\ce{pH}$ au point initial
On utilise la formule du $\ce{pH}$ pour un acide fort, en insérant la molarité initiale de l'acide.
$\ce{pH}=-log(\ce{[H3O+]})=-log(7,5\times 10^{-2})=1,1$
Points après adjonction de base (avant le point d'équivalence)
Le nombre d'ions $\ce{H3O+}$ diminue du fait de la neutralisation donc le $\ce{pH}$ augmente. Dans le tableau, nous donnons un exemple de calcul pour un volume de $\ce{NaOH}$ ajouté de $\ce{3,75\,\mathrm{mL}}$. Le nombre de moles de $\ce{NaOH}$ correspond à $3,75\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=3,75\times 10^{-4}\,\mathrm{mol}$.
| $\qquad\ce{HCl}$ | $\qquad+$ | $\qquad\ce{NaOH}$ | $\qquad\ce{->}$ | $\qquad\ce{NaCl}$ | $\qquad+$ | $\qquad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\qquad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\qquad3,75\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes
$$ \ce{H3O+} $$
$\ce{pH}$ aux points après adjonction de la base (AVANT le point d'équivalence)
On utilise la formule du $\ce{pH}$ pour un acide fort, en insérant la nouvelle molarité de l'acide qui tient compte des moles restantes d'acide et aussi du volume total ($13,75\,\mathrm{mL})$. $$ \ce{pH}=-log(\ce{[H3O+]})=-log\left (\frac{3,75\times 10^{-4}}{13,75\times 10^{-3}}\right )=1,6 $$
Points après la neutralisation (après le point équivalent)
Nous avons un excès de base forte. Dans le tableau, nous donnons un exemple de calcul pour un volume de $\ce{NaOH}$ ajouté de $\ce{11,25\,\mathrm{mL}}$. Le nombre de moles de $\ce{NaOH}$ correspond à $11,25\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=11,25\times 10^{-4}\,\mathrm{mol}$
| $\qquad\ce{HCl}$ | $\qquad+$ | $\qquad\ce{NaOH}$ | $\qquad\ce{->}$ | $\qquad\ce{NaCl}$ | $\qquad+$ | $\qquad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\qquad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\qquad11,25\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes :
$$ \ce{OH^{-}} $$
$\ce{pH}$ aux points après adjonction de la base (APRES le point d'équivalence)
On utilise la formule du $\ce{pH}$ pour une base forte, en insérant la molarité de la base qui tient compte des moles en excès de base et aussi du volume total ($21,25\,\mathrm{mL})$.
$$
\begin{array}{l}
\ce{pOH}=-log(\ce{[OH^{-}]})=-log\left (\frac{3,75\times 10^{-4}}{21,25\times 10^{-3}}\right )=1,8 \\
\ce{pH}=14-\ce{pOH}=14-1,8=12,2
\end{array}
$$
Point à l'infini
Le $\ce{pH}$ tend vers le $\ce{pH}$ de la base.
$$
\begin{array}{l}
\ce{pOH}=-log(\ce{[OH^{-}]})=-log(0,1)=1,0 \\
\ce{pH}=14-\ce{pOH}=14-1,0=13,0
\end{array}
$$
Courbe de neutralisation d'un acide FAIBLE par une base forte
Soit la neutralisation de $\ce{CH3COOH}$ par $\ce{NaOH}$ : $\ce{CH3COOH + NaOH → CH3COONa + H2O}$.
Le volume initial de solution acide est de $10\,\mathrm{mL}$ et la molarité de la solution titrante de $\ce{NaOH}$ est de $0,1\,\mathrm{M}$.
La procédure pour le calcul du $\ce{pH}$ est identique à celle suivi précédemment pour le titrage de l'acide fort: les particules dominantes n'étant en revanche pas les mêmes, les valeurs du $\ce{pH}$ seront différentes, jusqu'au point d'équivalence.

Courbe de neutralisation d'un acide fort par une base forte.
Point d'équivalence
La quantité de titrant ($\ce{NaOH}$) ajouté est égale à la quantité initiale d'acide: on peut écrire que $\ce{mol_{i}} = \ce{mol_{NaOH}}$.
Le volume correspondant au point d'équivalence est égal à $7,5\,\mathrm{mL}$. Cela correspond à $7,5\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=7,5\times 10^{-4}\,\mathrm{mol}$ de $\ce{NaOH}$ . S'agissant du point d'équivalence, ce nombre donne également le nombre de moles initiales d'acide. Nous pouvons ainsi calculer la molarité initiale de la solution acide, comme suit: $\frac{7,5\times 10^{-4}\,\mathrm{mol}}{1\times 10^{-2}\,\mathrm{L}}=0,075\,\mathrm{\frac{mol}{L}}$.
On étudie la variation provoquée par cette addition de $\ce{NaOH}$.
| $\quad\ce{CH3COOH}$ | $\quad+$ | $\quad\ce{NaOH}$ | $\quad\ce{->}$ | $\quad\ce{CH3COONa}$ | $\quad+$ | $\quad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\quad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\quad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes
$\ce{CH3COO-}$. Il s'agit de la base conjuguée de l'acide initial, qui ne peut pas être négligée (pensez à l'équilibre qui s'établit entre l'acide faible et sa base conjuguée).
$\ce{pH}$ au point d'équivalence
La base conjuguée agit en tant que base faible. Nous allons employer la formule des bases faibles, en insérant la molarité de la base conjuguée au point d'équivalence et le $pK_\mathrm {ab}$ du couple acide/base. $$ \ce{pH}=\frac{1}{2}(pK_{\mathrm {ab}}+14+log(C_b) )=\frac{1}{2}\left(4,75+14+log\left(\frac{7,5\times 10^{-4}}{17,5\times 10^{-3}}\right)\right ) =8,7 $$
Point initial
Le $\ce{pH}$ avant d'ajouter de la base ($V_{\ce{NaOH}} = 0\,\mathrm{mL}$) est égal au $\ce{pH}$ de la solution acide :
Particules dominantes
$$ \ce{CH3COOH} $$
$\ce{pH}$ au point initial
On utilise la formule du $\ce{pH}$ pour un acide faible, en insérant la molarité initiale de l'acide (acide faible).
$$
\ce{pH}=\frac{1}{2}(pK_{\mathrm {ab}}-log(C_a) )=\frac{1}{2}\left(4,75-log\left(7,5\times 10^{-2}\right)\right ) =2,9
$$
Points après adjonction de base (avant le point d'équivalence)
Le nombre de molécules de $\ce{CH3COOH}$ diminue du fait de la neutralisation: ces molécules seront converties dans la base conjuguée $\ce{CH3COO-}$ . La coexistence des particules acide $\ce{CH3COOH}$ et basique $\ce{CH3COO-}$ aboutit à la formation d'une solution tampon.
Dans le tableau, nous donnons un exemple de calcul pour un volume de $\ce{NaOH}$ ajouté de $\ce{3,75\,\mathrm{mL}}$. Le nombre de moles de $\ce{NaOH}$ correspond à $3,75\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=3,75\times 10^{-4}\,\mathrm{mol}$. Ce point correspond à un volume de titrant ajouté égal à la moitié du volume nécessaire pour l'équivalence: il se nomme ainsi point de demi-équivalence.
L'approche que nous allons suivre s'applique au points avant l'équivalence et en particulier dans le plateau de la courbe.
| $\quad\ce{CH3COOH}$ | $\quad+$ | $\quad\ce{NaOH}$ | $\quad\ce{->}$ | $\quad\ce{CH3COONa}$ | $\quad+$ | $\quad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\quad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\quad3,75\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes
$$ \ce{CH3COOH}\quad \mathrm{et}\quad \ce{CH3COO-} $$
$\ce{pH}$ au points après adjonction de la base (AVANT le point d'équivalence)
On utilise la formule du $\ce{pH}$ pour un tampon, en insérant la molarité de l'acide et de sa base conjuguée, après avoir calculé des moles restantes d'acide et les moles formées de base.
$$
\ce{pH}=pK_\mathrm {ab}+log\left(\frac{\frac{3,75\times 10^{-4}}{13,75\times 10^{-3}}}{\frac{3,75\times 10^{-4}}{13,75\times 10^{-3}}}\right) = 4,75+log\left(1\right) =4,75
$$
Notez pour le calcul du $\ce{pH}$ d'une solution tampon, le volume est superflu.
Notez également que le $\ce{pH}$ au point de demi-équivalence donne le $pK_\mathrm {ab}$ et permet donc d'identifier le couple acide/base.
Points après la neutralisation (après le point équivalent)
Nous avons un excès de base forte. Dans le tableau, nous donnons un exemple de calcul pour un volume de $\ce{NaOH}$ ajouté de $\ce{11,25\,\mathrm{mL}}$. Le nombre de moles de $\ce{NaOH}$ correspond à $11,25\times 10^{-3}\mathrm{L}\,\cdot 0,1\,\mathrm{\frac{\mathrm{mol}}{\mathrm{L}}}=11,25\times 10^{-4}\,\mathrm{mol}$
| $\quad\ce{CH3COOH}$ | $\quad+$ | $\quad\ce{NaOH}$ | $\quad\ce{->}$ | $\quad\ce{CH3COONa}$ | $\quad+$ | $\quad\ce{H2O}$ | |
|---|---|---|---|---|---|---|---|
| $\ce{mol_{i}}$ | $\quad7,5\times 10^{-4}$ | ||||||
| $\ce{mol_{NaOH}}$ | $\quad11,25\times 10^{-4}$ | ||||||
| $\ce{mol_{{v}}}$ | |||||||
| $\ce{mol_{f}}$ |
Particules dominantes :
$$ \ce{OH^{-}} $$
$\ce{pH}$ aux points après adjonction de la base (APRES le point d'équivalence)
On utilise la formule du $\ce{pH}$ pour une base forte, en insérant la molarité de la base qui tient compte des moles en excès de base et aussi du volume total ($21,25\,\mathrm{mL})$.
$$
\begin{array}{l}
\ce{pOH}=-log(\ce{[OH^{-}]})=-log\left (\frac{3,75\times 10^{-4}}{21,25\times 10^{-3}}\right )=1,8 \\
\ce{pH}=14-\ce{pOH}=12,2
\end{array}
$$
Point à l'infini
Le $\ce{pH}$ tend vers le $\ce{pH}$ de la base.
$$
\begin{array}{l}
\ce{pOH}=-log(\ce{[OH^{-}]})=-log(0,1)=1,0 \\
\ce{pH}=14-\ce{pOH}=14-1,0=13,0
\end{array}
$$
Les indicateurs
Un indicateur est une substance qui existe sous deux formes différentes en solution acide et basique. En général, c'est un acide ou une base faible dont la forme acide possède une couleur différente de la forme basique. On peut écrire l'équilibre suivant :
$$ \begin{array}{l} \ce{HIn}\rightleftharpoons \ce{In- + H+} \\ \ce{K_{in}}=\frac{\ce{[In^{-}] \cdot [H+]}}{\ce{[HIn]}} \end{array} $$
Le $\ce{pH}$ auquel l'indicateur est présent à $50\,\%$ sous forme $\ce{In^{-}}$ et $50\,\%$ sous forme $\ce{InH}$ s'appelle le point de virage (zone tampon), où l'on aura:
$$ \ce{[In^{-}] = [HIn]}\Rightarrow \ce{pK_{in}=pH} $$
Au $\ce{pH = pK_{in} – 1}$, l'indicateur sera à $90\,\%$ sous forme acide et donnera sa coloration acide, au $\ce{pH = pK_{in} + 1}$, l'indicateur sera à $90\,\%$ sous forme basique et donnera sa coloration basique.
L'Indicateur montre donc son virage de couleur dans une gamme de $2$ unités de $\ce{pH}$. Le choix de l'indicateur est fait de façon à ce que ce virage ait lieu près du point d'équivalence.
Voici quelques exemple d'indicateur.
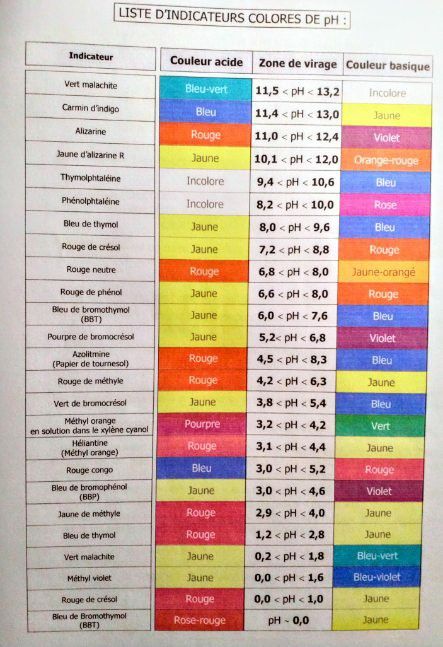
Une liste des indicateurs acide/base les plus courants.
Exercices SERIE Neutralisation Acide Base
$100\,\mathrm{mL}$ d'une solution de $\ce{LiOH}$ sont neutralisés exactement par $50\,\mathrm{mL}$ de $\ce{HNO3}$ $10^{- 1}\,\mathrm{mol/L}$
Quel est le $\ce{pH}$ de la solution de $\ce{HNO3}$ ?
Quel est le $\ce{pH}$ de la solution avant la neutralisation ?
Tracer l'allure générale de la courbe (en indiquant clairement les points connus).
Donner l'allure générale d'une courbe de neutralisation de $20\,\mathrm{mL}$ de $\ce{NaOH}$ $0,1\,\mathrm{mol/L}$ par du $\ce{H2SO4}$ $0,2\,\mathrm{mol/L}$ en indiquant clairement le pH du départ, le $\ce{pH}$ à la fin ainsi que le point équivalent ($\ce{pH}$ et $V_a$).
En neutralisant $15\,\mathrm{mL}$ de $\ce{H2SO4}$ on a obtenu la courbe suivante :

Courbe de neutralisation d'une solution de $\ce{H2SO4}$ par une base forte.
Calculer la molarité de l'acide.
Vers quelle valeur va tendre le $\ce{pH}$ final, calculez-le.
Calculer le $\ce{pH}$ initial.
Quelles sont les particules présentes après adjonction de : $15\,\mathrm{mL}$ de $\ce{NaOH}$, $20\,\mathrm{mL}$ de $\ce{NaOH}$, $30\,\mathrm{mL}$ de $\ce{NaOH}$.
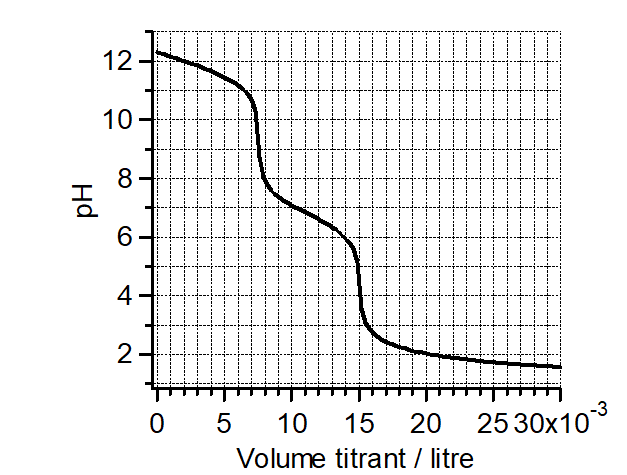
Soit la courbe de neutralisation suivante. Sachant qu'au point équivalent, on a des ions $\ce{Mg^{2+}}$ et $\ce{NO3-}$ dans l'eau.

Courbe de neutralisation d'une solution de $\ce{HNO3}$ par une base forte.
Écrire l'équation de la réaction.
Avec quel réactif a-t-on neutralisé la solution initiale ?
Vers quelle valeur va tendre le $\ce{pH}$ final si la concentration du réactif (=titrant) est $10^{-3}\,\mathrm{mol/L}$ ?
Quel est le pH initial sachant qu'on avait $20\,\mathrm{mL}$ de solution ?
Quel volume d'acide chlorhydrique à $0,1\,\mathrm{mol/L}$ faut-il verser dans $100\,\mathrm{mL}$ d'ammoniaque $5\times 10^{-2}\,\mathrm{mol/L}$ pour que le $\ce{pH}$ soit égal au $pK_\mathrm {ab}$ du couple $\ce{NH4+/NH3}$ ?
Quel indicateur doit-on utiliser pour titrer de l'ammoniaque (~ $1\,\mathrm{mol/L}$) par du $\ce{HCl}$ ?
Dans la titration de l'acide acétique (~ $1\,\mathrm{mol/L}$) par de la soude, que conseillez-vous comme indicateur ?
On veut doser l'acide ascorbique ($\ce{AH}$) dans un échantillon de médicament ($10\,\mathrm{mL}$) par la soude ($0,15\,\mathrm{mol/L}$). La courbe de neutralisation est obtenue en suivant la variation du pH selon la base ajoutée. De cette courbe, déterminez :

Courbe de neutralisation d'une solution d'acide ascorbique par la soude.
Si c'est un acide fort ou faible.
Quel est son $pK_\mathrm {ab}$.
Les produits chimiques aux points initial, de demi-équivalence, d'équivalence.
L’indicateur que l'on doit utiliser pour un titrage visuel.
La molarité de l'acide ascorbique.
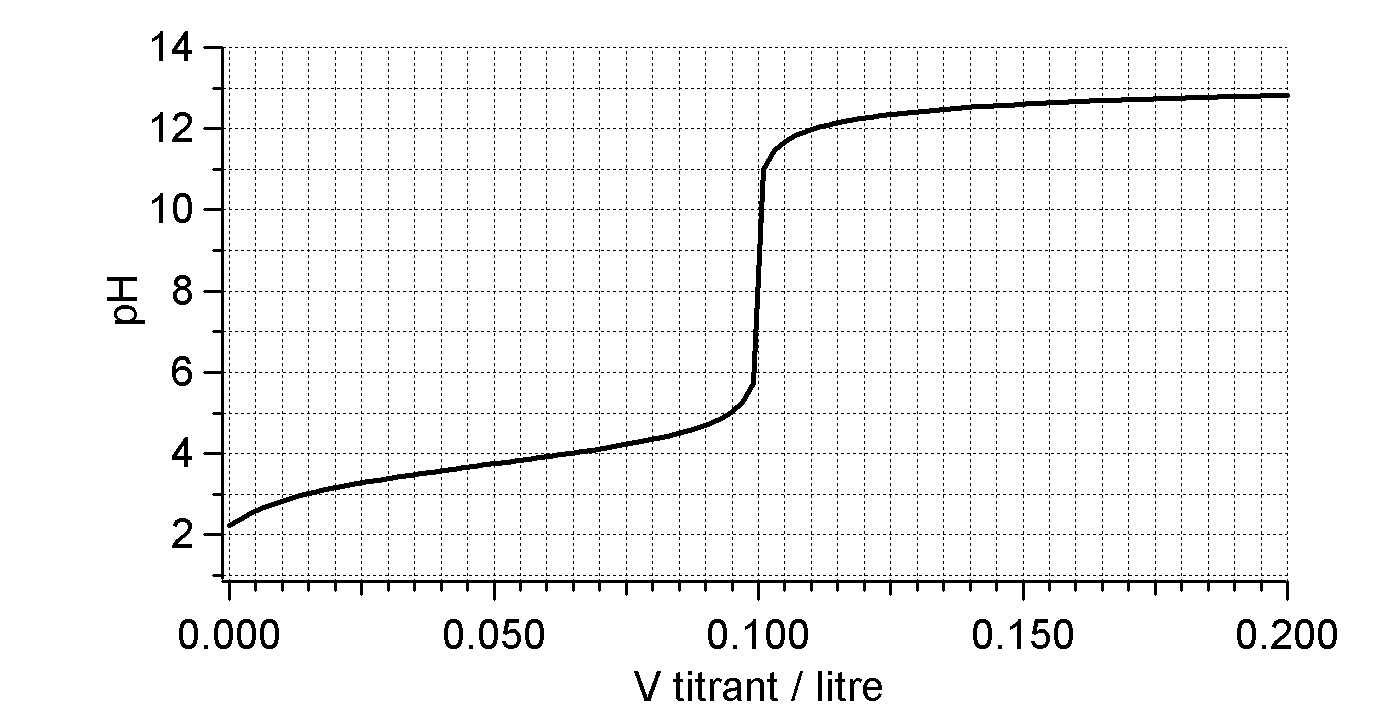
Soit la courbe de neutralisation de $10\,\mathrm{mL}$ d'acide phosphorique par du $\ce{NaOH}$ $0,1\,\mathrm{mol/L}$.
Courbe de neutralisation d'une solution d'acide phosphorique par $\ce{NaOH}$.
Déterminez la concentration de l'acide.
Complétez le tableau suivant :
| Point | Nom des points | Espèce(s) chimique(s) | $\ce{pH}$ |
|---|---|---|---|
Indiquez dans quelle zone de virage doit se trouver les indicateurs visuels utilisés pour la 1ère et 2ème neutralisation.
Déterminez le $\ce{pH}$ après avoir introduit $12\,\mathrm{mL}$ de $\ce{NaOH}$.
Déterminez le $\ce{pH}$ après avoir introduit $22\,\mathrm{mL}$ de $\ce{NaOH}$.
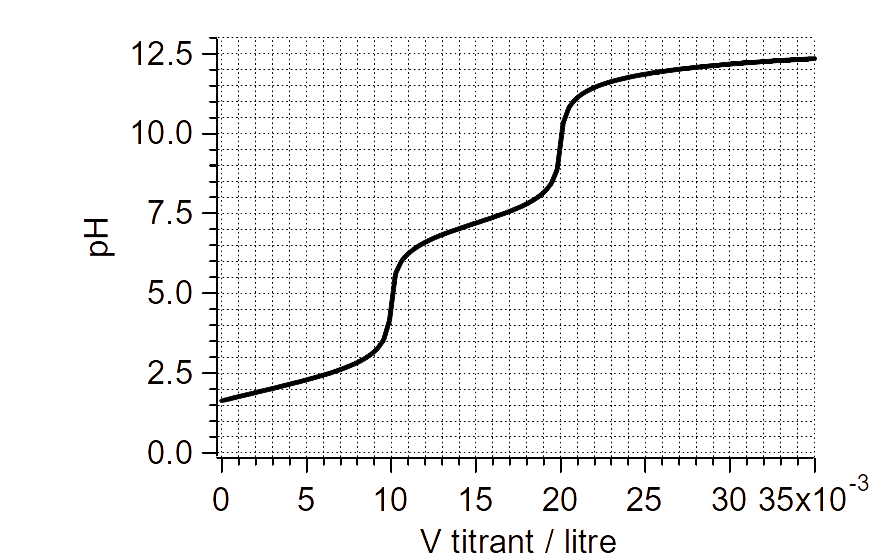
Soit la courbe de titration de $10\,\mathrm{mL}$ de $\ce{Na3PO4}$ par du $\ce{HCl}$ $0,1\,\mathrm{mol/L}$.
Courbe de neutralisation d'une solution de phosphate de sodium par $\ce{HCl}$.
Quel est le volume de $\ce{HCl}$ nécessaire à la neutralisation complète et quelle est la concentration de la base ?
Complétez le tableau suivant :
| Point | Nom des points | Espèce(s) chimique(s) | $\ce{pH}$ |
|---|---|---|---|
Calculez le $\ce{pH}$ de la solution lorsque $15\,\mathrm{mL}$ de $\ce{HCl}$ sont ajoutés.
Quel est le $\ce{pH}$ d'un mélange contenant $0,2\,\mathrm{mol}$ de $\ce{NH4Cl}$ et $0,1\,\mathrm{mol}$ de $\ce{NaOH}$ dans $1$ litre.
Répondez aux questions suivantes:
Quelle est la concentration d'une solution de $\ce{NH4Cl}$ dont le $\ce{pH}$ est de $5,1$ ?
Calculez le volume de $\ce{NaOH}$ $0,2\,\mathrm{mol/L}$ qu'il faut ajouter à $250\,\mathrm{mL}$ de $\ce{NH4Cl}$ pour avoir une solution tampon à $\ce{pH = 9}$ ?
On dose $10\,\mathrm{mL}$ d'un mélange de $\ce{HBr}$ et de $\ce{CH3COOH}$ par du $\ce{NaOH}$ $0,1\,\mathrm{mol/L}$. La courbe de titration présente $2$ points d'équivalence à $12\,\mathrm{mL}$ et $22\,\mathrm{mL}$ de $\ce{NaOH}$. (Aide : au premier point d’équivalence, seulement le $\ce{H+}$ de $\ce{HBr}$ est neutralisé)
Donnez la composition du mélange.
Donnez le $\ce{pH}$ aux points équivalents.
Déterminez la concentration de l’acide acétique.
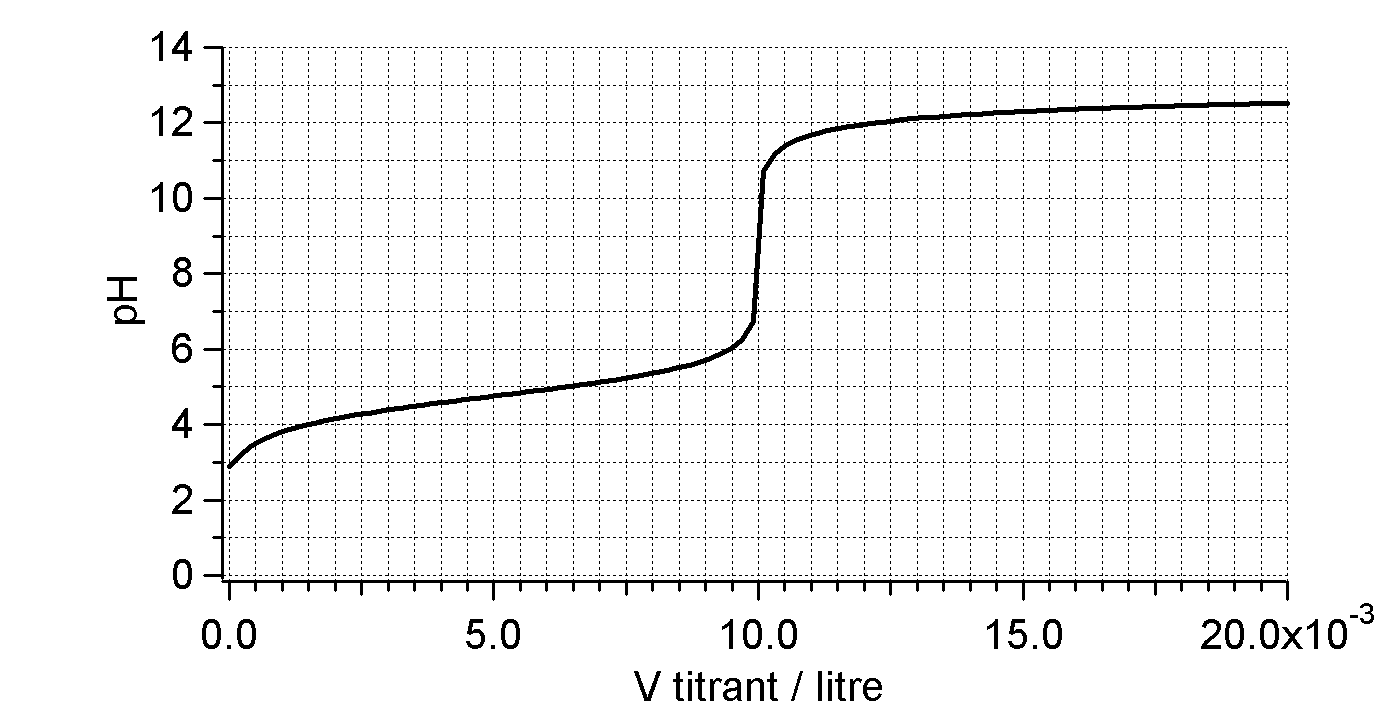
Neutralisation de $10\,\mathrm{mL}$ d’acide acétique ( ??? $\mathrm{M}$) par $\ce{NaOH}$ ($0,1\,\mathrm{M}$).
Déterminez l’acide et sa concentration.
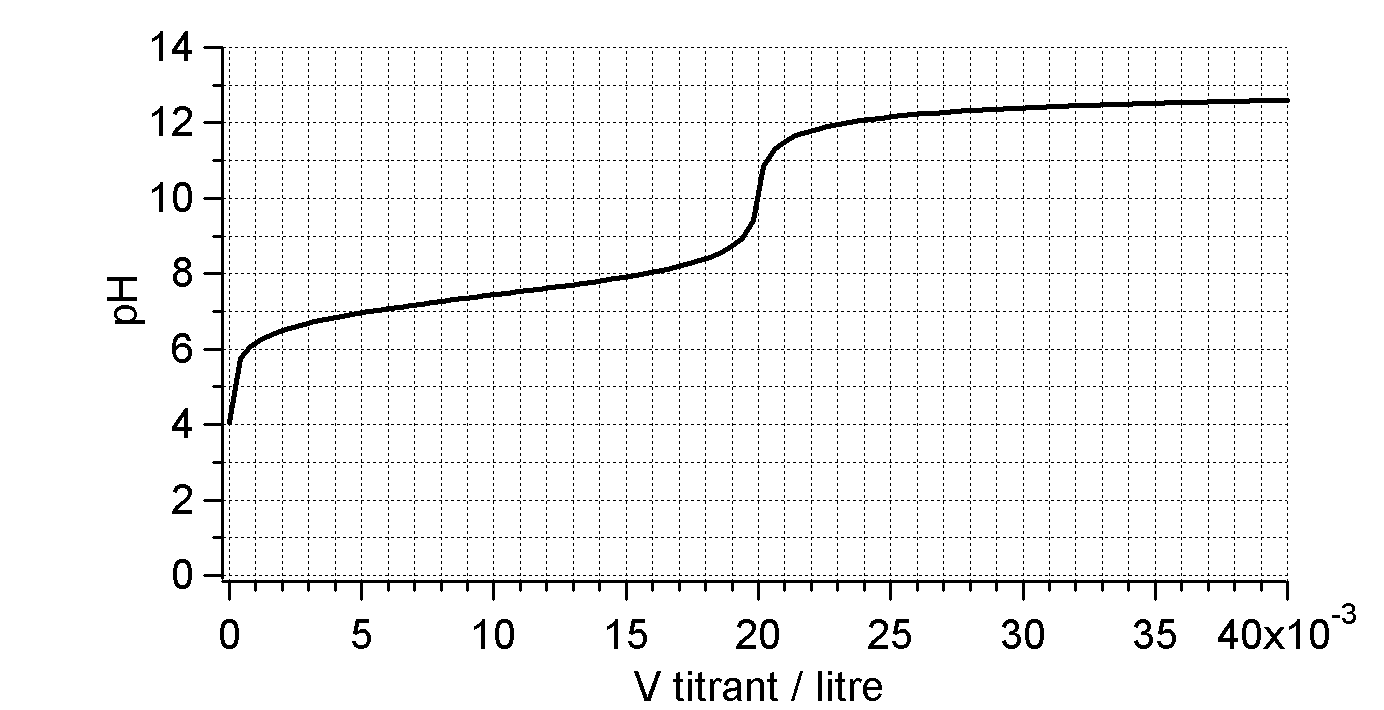
Neutralisation de $10\,\mathrm{mL}$ d’acide ?????? ( ??? $\mathrm{M}$) par $\ce{NaOH}$ ($0,1\,\mathrm{M}$)
Déterminez la concentration de la base.
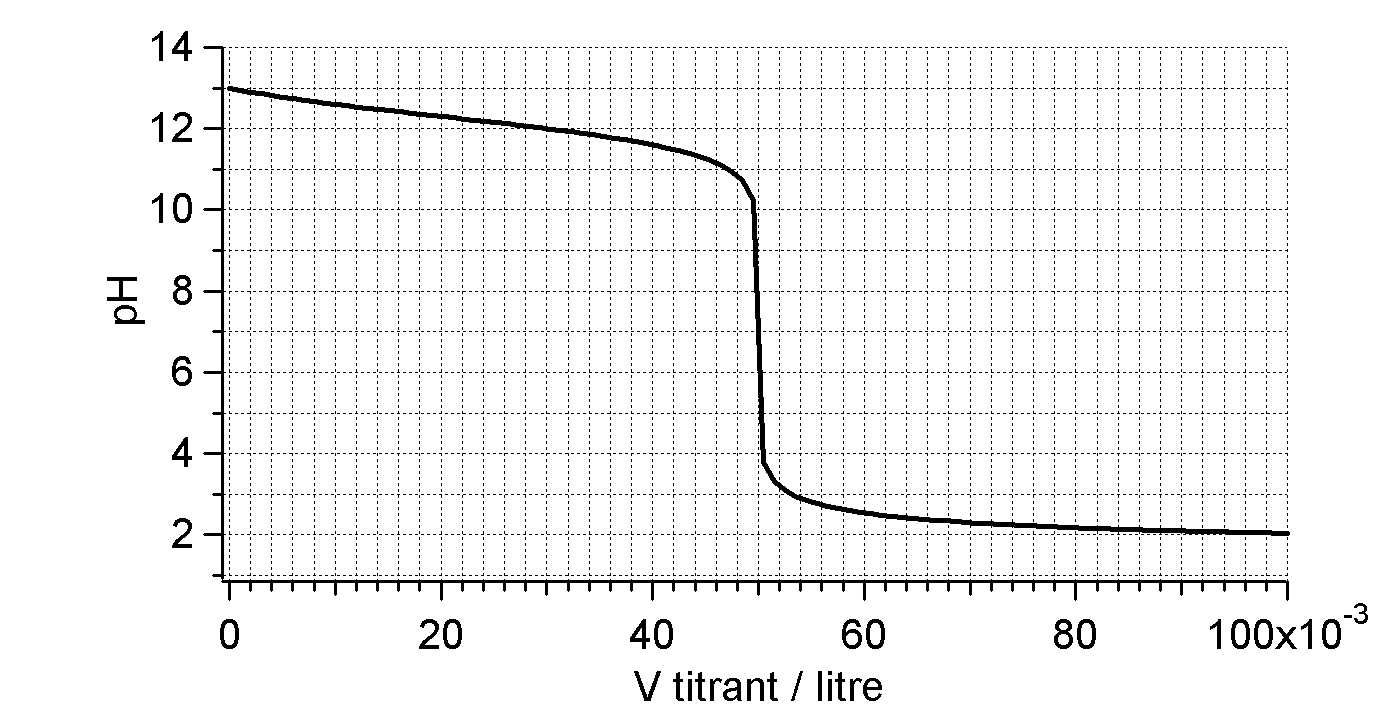
Neutralisation de $10\,\mathrm{mL}$ de $\ce{NaOH}$ ?????? ( ??? $\mathrm{M}$) par $\ce{HCl}$ ($0,02\,\mathrm{M}$)
Déterminez la concentration de la base et la base.
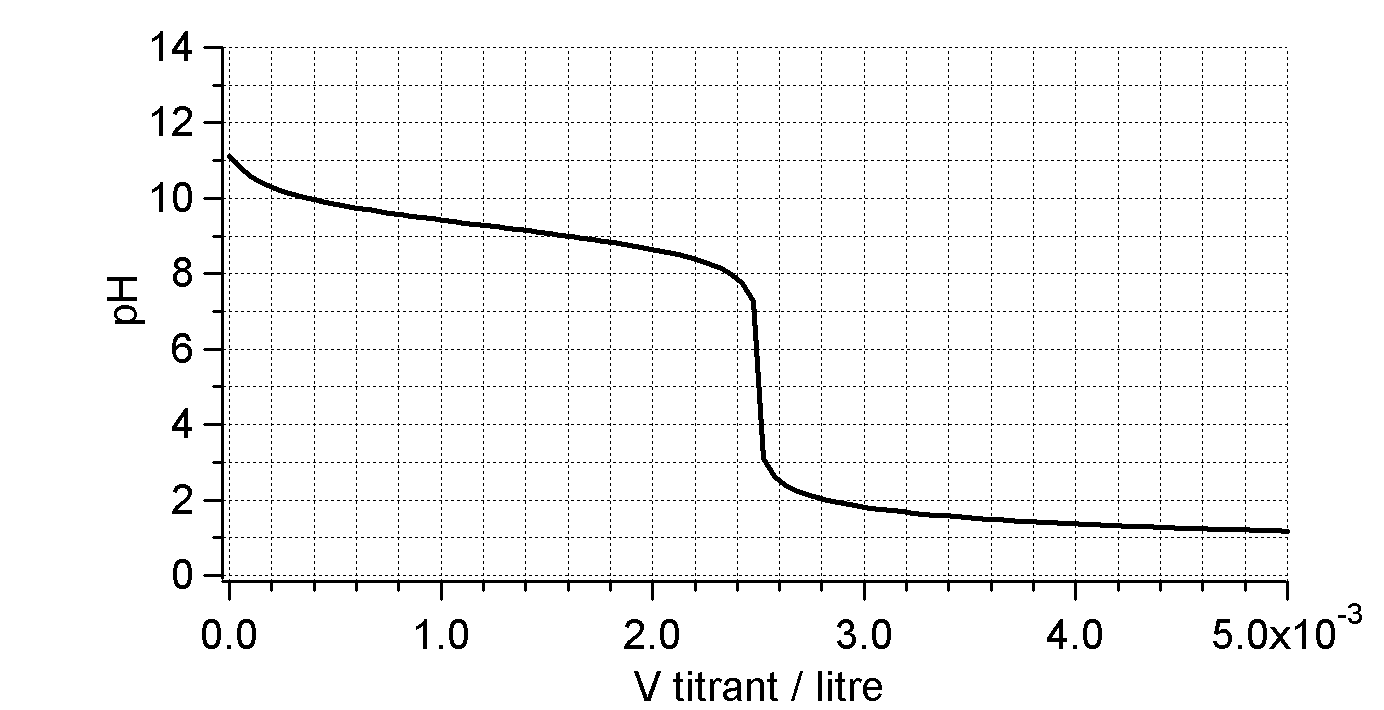
Neutralisation de $10\,\mathrm{mL}$ de ?????? ( ??? $\mathrm{M}$) par $\ce{HCl}$
($0,4\,\mathrm{M}$)
Déterminez la concentration de la susbtance dissoute dans l'eau et trouvez-la.
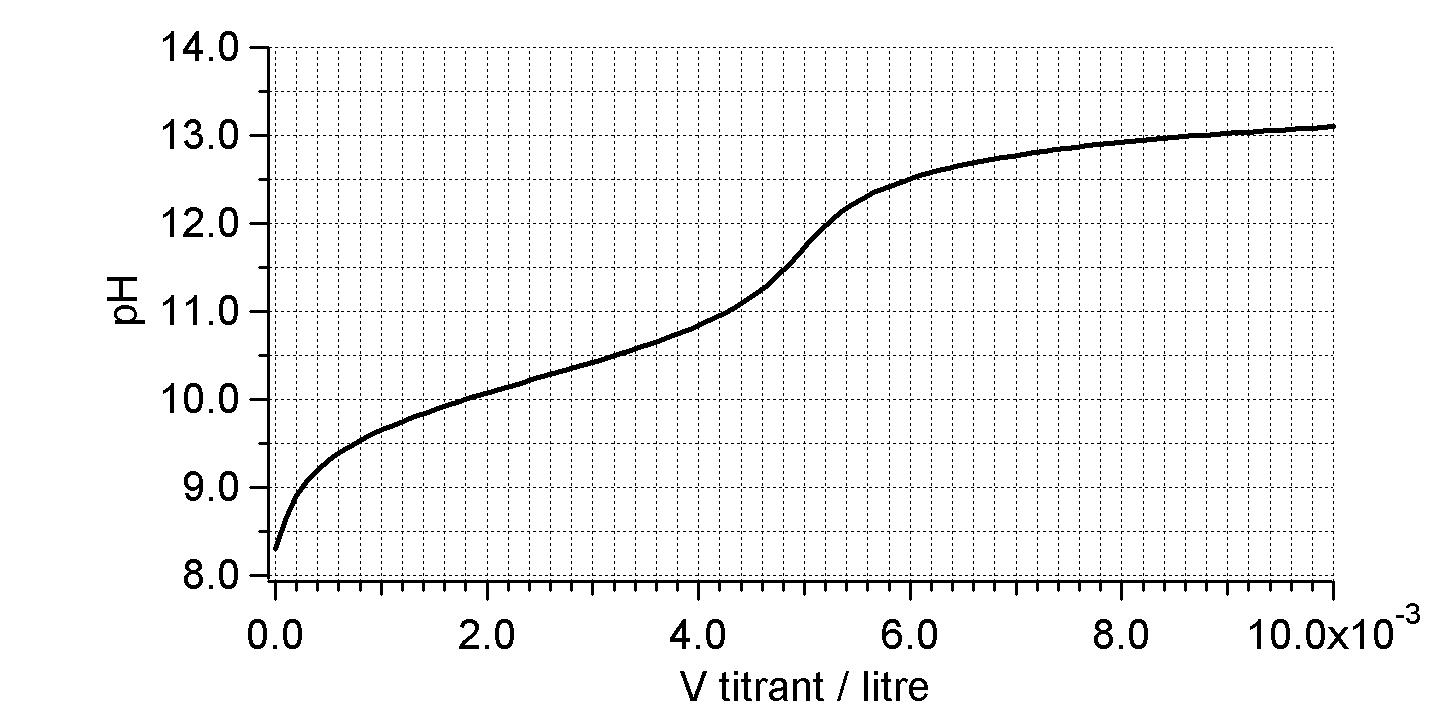
Neutralisation de $10\,\mathrm{mL}$ de ?????? ( ??? $\mathrm{M}$) par $\ce{NaOH}$
($0,5\,\mathrm{M}$)
Déterminez la concentration de l’acide et l’acide.
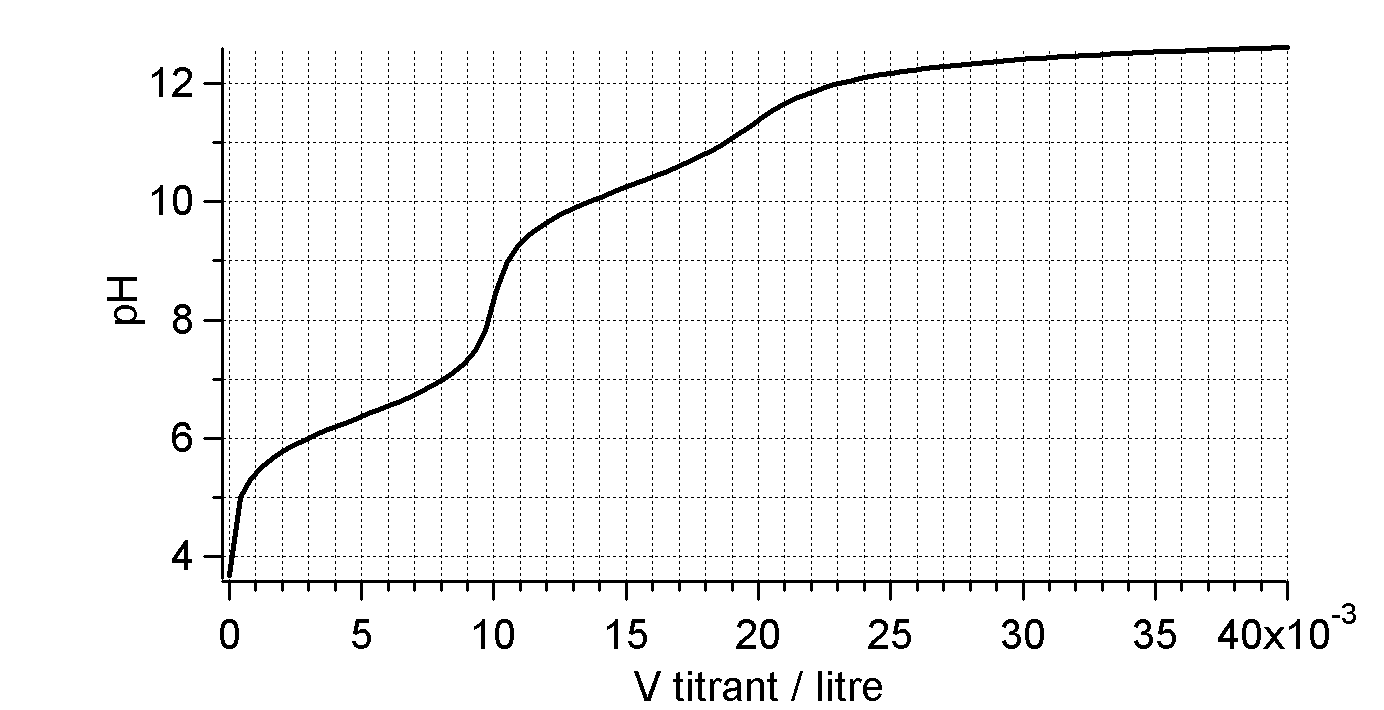
Neutralisation de $10\,\mathrm{mL}$ d’acide ?????? ( ??? $\mathrm{M}$) par $\ce{NaOH}$ ($0.1\,\mathrm{M}$)