Masses et moles
Un chimiste est très souvent appelé à déterminer des quantités. Par exemple, il peut s'interroger sur la problématique suivante, de très grande actualité, qui est liée à l'accumulation du plastique dans l'environnement. Voici, à ce sujet, une première question, de type qualitatif, qu'on s'est posée en 1ère année.
Comment transformer le plastique usagé en quelque chose d'utile (exemple: un combustible), qui sera plus tard réutilisé pour d'autres applications ?
Et voici un exemple de question de type quantitatif qu'on se posera au cours de ce chapitre:
Combien de combustible peut-on obtenir à partir d'$1\,\mathrm{kg}$ de plastique ?
L'objectif de ce chapitre est d'appréhender les outils qui nous permettront d'obtenir :
- la quantité obtenue d'un produit, à partir de la quantité employée d'un réactif.
- la quantité d'un réactif nécessaire pour obtenir une quantité désirée d'un produit.
Les atomes existent ! Comment le sait-on ?
Atomes dans un objet
D'abord une question pour rafraîchir le programme de la première année:
Y a-t-il plus d'atomes dans une bague en or qui pèse $10\,\mathrm{g}$ ou dans une autre en argent qui a exactement le même poids ? Développez votre réponse.
Dans $1$ mole d'or ou dans $1$ mole d'argent: où est-ce qu'il y a plus d'atomes ?
Atomes dans une réaction chimique !
Comment a-t-on prouvé que les ATOMES existent ? ($\ce{S}$=soufre, $\ce{Fe}$=fer)
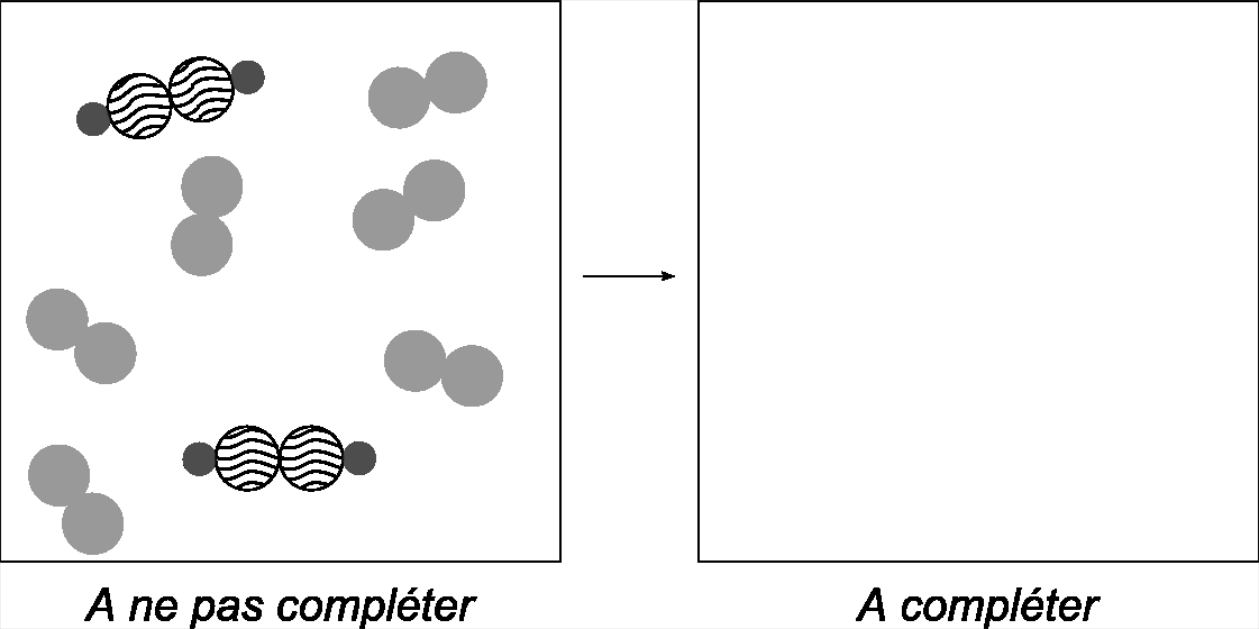
Observez les images ci-dessous dans lesquelles les expériences de Proust sont présentées.
Décrivez les deux expériences illustrées ci-dessous et complétez ensuite l'image

L'expérience de Proust: on change la quantité de soufre, mais on maintient la quantité de fer: l'on obtient la même quantité de $\ce{FeS}$ ... bizarre !? ...
On double la quantité de soufre et aussi celle de fer. Les proportions de l'expérience (m1) sont maintenues. Quelle quantité de $\ce{FeS}$ obtiendra-t-on ?

On double la quantité de soufre et aussi la quantité de fer: quelle quantité de $\ce{FeS}$ va-t-on obtenir ?
Le travail de Proust et d'autres scientifiques du IXème siècle ont fourni les premières preuves de l'existence des atomes: comment expliquer en effet que, pour ne pas avoir de "reste", il faille employer des quantités de $\ce{S}$ et $\ce{Fe}$ dans une proportion bien précise, celle donnée par le rapport de
$$ \frac{masse\,de\,\ce{S}}{masse\,de\,\ce{Fe}}=\frac{3,2\,\mathrm{g}}{5,6\,\mathrm{g}} $$
L'hypothèse qui fut avancée à l'époque est que, dans ces deux masses, il y a le même nombre d'atomes et qu'un atome de $\ce{S}$ n'a pas la même masse qu'un atome $\ce{Fe}$.
Réactions de précipitation
Voici un rappel des réactions de précipitation. A vous de réviser cette partie qui était dans le programme de la 1ère année.

Les composés ioniques ou fortement polaires se dissocient dans l'eau. On nomme ce phénomène, la dissociation électrolytique.
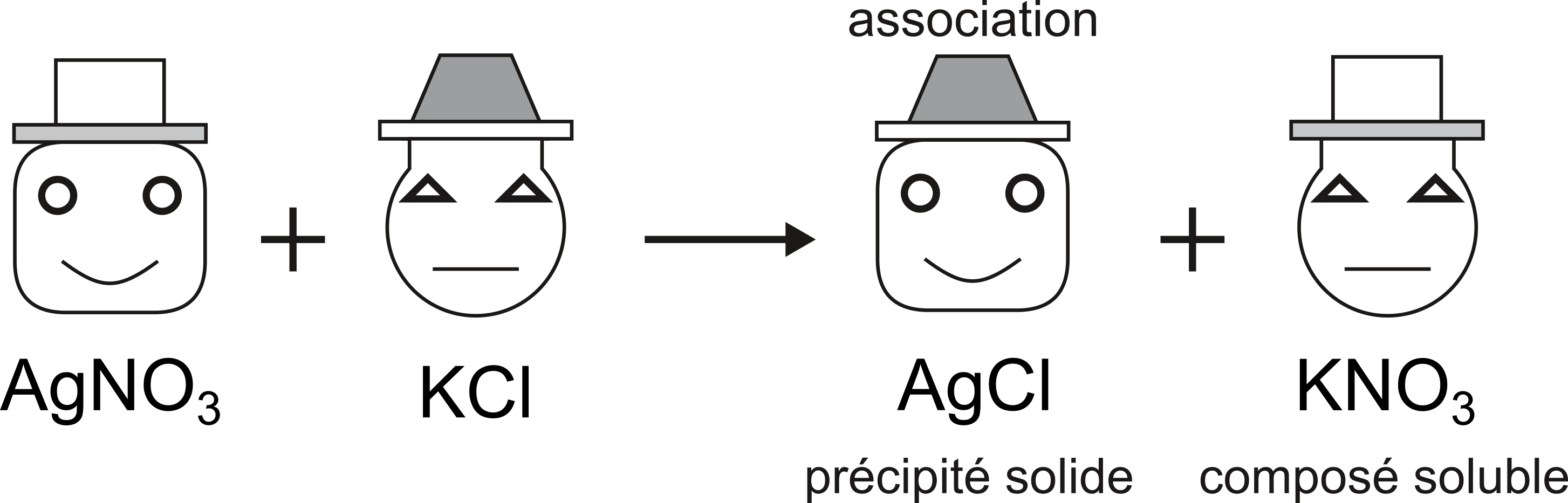
Et voici le déplacement qui mène à la précipitation d'un composé insoluble dans l'eau, nommé le précipité. Le composé soluble reste en solution, sous forme d'ions séparés.
Définition de réaction de précipitation: réaction ionique qui se produit quand les deux ions (cation et anion) d'une molécule insoluble se rencontrent. Ces deux ions se combinent pour former une molécule et donnent un solide appelé précipité.
Les particules constituant l’atome et leur masse
Il n'est pas nécessaire de retenir la valeur de la masse de l'électron. Par contre il est utile de savoir que cette masse est beaucoup plus petite que celle d'un nucléon (environ $2000$ fois plus petite) ce qui nous autorise à négliger la masse des électrons devant celle des nucléons. La masse absolue des atomes importe peu au chimiste qui ne doit connaître que la masse relative des atomes. La masse relative est la masse comparée à la masse d'un atome déterminé, prise comme unité. Parmi différentes possibilités, on a adopté en $1961$ le carbone (isotope $12$) comme base de calcul des masses atomiques. Définition : l'unité de masse atomique ($\mathrm{u}$) est exactement le douzième de la masse d'un atome de carbone.
$$ 1\,\mathrm{u} = 1,661\times 10^{-27}\,\mathrm{kg} $$
Comme les électrons ont une masse négligeable, la masse des protons ajoutée à la masse des neutrons donne la masse atomique qui est généralement exprimée en
unité de masse atomique ($\mathrm{u}$).
Une nouvelle unité de quantité de matière: la mole
Nécessité d'un changement d'échelle
La masse d'un atome où d'une molécule est très petite (de l'ordre de $10^{-26}\,\mathrm{kg}$). De ce fait, les réactions chimiques font intervenir un nombre considérable d'entités chimiques. A titre d'exemple, un clou en fer de masse $12,46\,\mathrm{g}$ contient environ $1,31\times 10^{23}$ atomes. Le nombre obtenu n'est évidemment pas pratique à manipuler car il s'agit d'un nombre extrêmement grand. Ce calcul met en évidence la nécessité d'introduire une nouvelle échelle, plus commode, pour manipuler des quantités de matière en chimie. D’ailleurs, les balances au laboratoire nous ne permettraient de mesurer la masse d’un atome ou d’une molécule.
La mole: ancienne définition
D'après ce qui précède, il est nécessaire de définir une nouvelle unité de quantité de matière:
Une MOLE représente une quantité de matière composée d'autant d'entités qu'il y a d'atomes dans $12,00\,\mathrm{g}$ de carbone $12$.
Nombre d'Avogadro
Le nombre d'atomes contenus dans une mole de carbone $12$ est appelé nombre d'Avogadro et sera noté $N_A$.
$$ N_A=6,022\times 10^{23}\,\mathrm{mol}^{-1} $$
La définition adoptée en $2019$ est la suivante: une mole représente une quantité de matière composée de $6,022\times 10^{23}$ entités élémentaires (= atomes, molécules, électrons … cela dépend du type d'échantillon étudié).
Masses molaires ($M$)
Masse molaire atomique
La masse molaire atomique d'un élément est la masse d'une mole d'atomes de cet élément, les proportions des différents isotopes étant celles que l'on rencontre dans la nature.
Exercice
$M(\ce{Cu})$=.......…………………. $\mathrm{g\cdot mol^{-1}}$; $\mathrm{M}(\ce{I})$=…....…………………….$\mathrm{g\cdot mol^{-1}}$.
Notez que l'unité de mesure sont les $\mathrm{g\cdot mol^{-1}}$ ($ = \mathrm{g/mol}$, donc $\mathrm{g}$ sur $\mathrm{mol}$): les grammes contenus dans une mole (= grammes par mole).
Masse molaire moléculaire
La masse molaire moléculaire est la masse d'une mole de molécules de l'espèce considérée. On la calcule en effectuant la somme des masses molaires atomiques des atomes qui constituent la molécule.
$M(\ce{H2O}) = 2\times M(\ce{H}) + M(\ce{O})$
$=> M(\ce{H2O}) = 2\times 1,0 + 16,0$
$=> M(\ce{H2O}) = 18,0\,\mathrm{g\cdot mol^{-1}}$
Conversion masse/mole
Comment peut-on passer des grammes au nombre de moles ? On divise la masse totale par la masse d'une mole (= masse molaire).
$$ \frac{masse}{masse\,\mathrm{mol}aire}=\mathrm{\frac{g}{\frac{g}{mol}}=g\cdot \frac{mol}{g}=mol} $$
Comment peut-on passer des moles aux grammes ? On multiplie le nombre de moles par la masse d'une mole (= masse molaire).
$$ mol\cdot masse\,\mathrm{mol}aire=\mathrm{mol\cdot \frac{g}{mol}=g} $$
Table de conversion
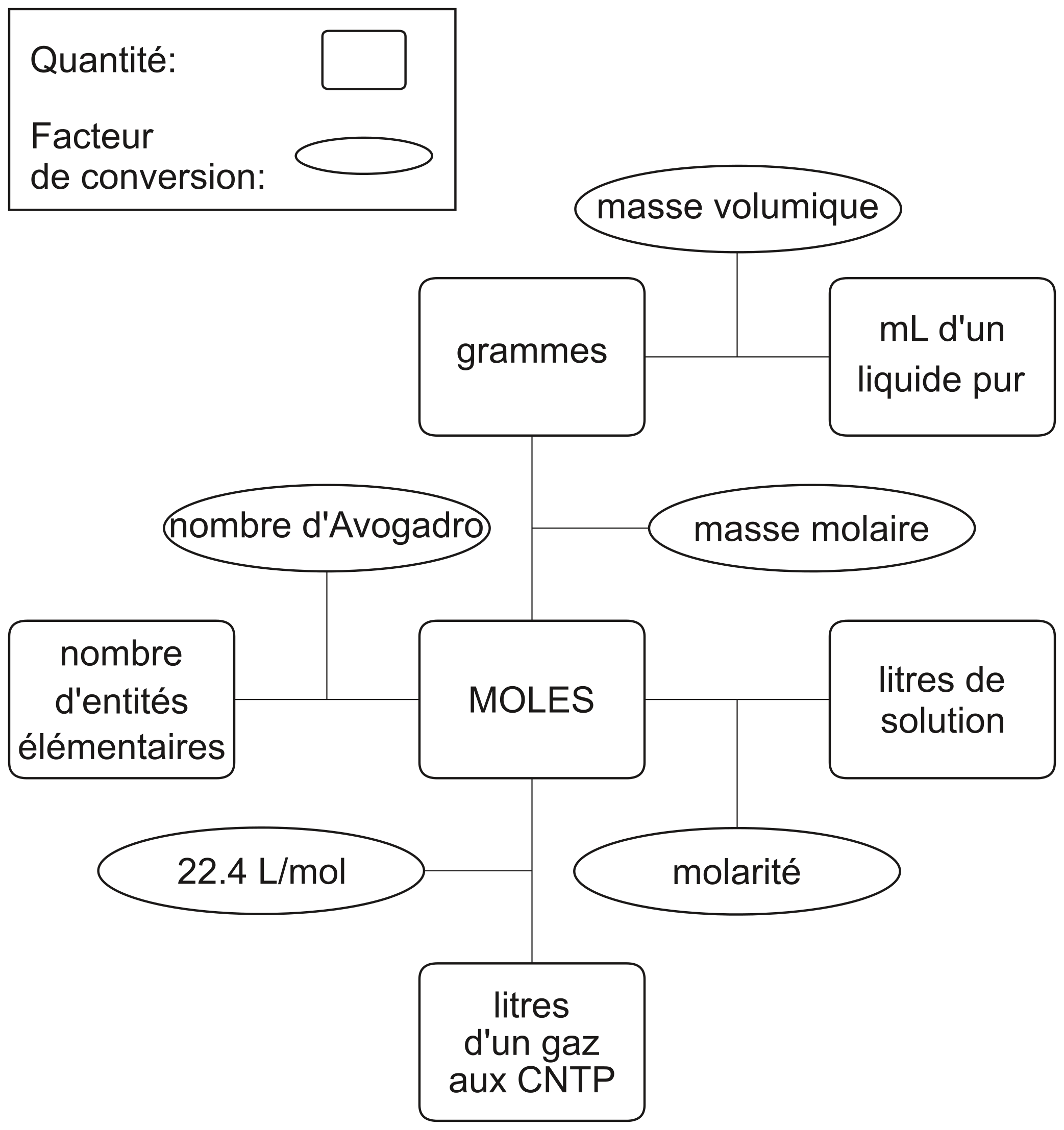
Les quantités étudiées en chimie et lurs facteurs de conversion
Dans cette table de conversion, figurent toutes les opérations que nous affronterons à partir de ce chapitre jusqu'à la fin ou presque de cette deuxième année. Elle demeure pour l'instant assez obscure: normal , il nous reste pas mal de choses à découvrir !
Nombre d'Avogadro ($6,022\times 10^{23}\,\mathrm{mol}^{-1}$): quelle énormité ! Sachant que la masse d'un grain de sable est égale à $8\times 10^{-5} \,\mathrm{g}$,
calculer la masse d'une mole de grains de sable.
La masse volumique du sable vaut $2,5\,\mathrm{g/cm^{3}}$. Déterminer le volume d'une mole de grains de sable.
Sachant que la surface du désert du Sahara est de $8\times 10^{6}\,\mathrm{km^2}$, calculer la profondeur à laquelle il faudrait creuser pour obtenir une mole de grains de sable et exprimer le résultat en mètres.
Exercices Masse et Matière SERIE A
Volume Molaire
Pour les substances gazeuses, il existe une relation simple entre leur quantité, la température à laquelle elles sont soumises, leur pression et leur volume. Cette relation, est appelée la loi des gaz parfaits :
$$ P\cdot V=n\cdot R\cdot T $$
$P$ : pression du gaz $[\mathrm{atm}]$
$V$ : volume du gaz [$\mathrm{L}$ = litre]
$n$ : nombre de moles de gaz $[\mathrm{mol}]$
$R$ = constante des gaz parfaits ($R = 8,206\times 10^{-2}\,[\mathrm{L\times atm\times mol^{-1}\times K^{-1}}]$)
$T$ : température $[\mathrm{K}]$ (en Kelvin; $T [\mathrm{K}] = T [\mathrm{^\circ C}] + 273$)
Il découle de la loi des gaz parfaits que, dans les conditions normales de température et de pression (CNTP; $T = 0\,°C$, $P = 1\,\mathrm{atm}$), $1$ mole de gaz occupe un volume de $22,4\,\mathrm{L}$ précisément, quelle que soit la nature de ce gaz.
Exercices :
Calculs de moles et masses
Rappel sur les équations de précipitation
Une bonne partie des exercices de ce chapitre propose des réactions de précipitation: voici donc un bref exercice de rappel sur le sujet.
Problèmes de chimie quantitative
Ils consistent à déduire la quantité d'un produit (en grammes ou en nombre de mole) connaissant la quantité d'un autre produit en grammes ou en nombre de mole.
Exercice:
Marche à suivre : création d'un tableau.
- Établir l'équation et équilibrer si nécessaire.
- Déduire, de l'équation, la proportion existante entre les moles que l'on connaît et les moles que l'on cherche.
- Déterminer les masses molaires des réactifs et des produits.
- Si on donne la quantité connue d'une substance (réactif ou produit) en grammes, chercher le nombre de moles correspondant (avec la masse molaire $M$).
- A partir des moles, remonter à la masse de la substance que l'on cherche à déterminer.
| $\ce{Al2(SO4)3}$ | + | $\ce{NaOH}$ | $\ce{->}$ | $...............$ | + | $...............$ | |
|---|---|---|---|---|---|---|---|
| proportions | |||||||
| mole $[\mathrm{mol}]$ |
|||||||
| masse molaire $[\mathrm{g\cdot mol^{-1}}]$ |
|||||||
| masse $[\mathrm{g}]$ |
Réactif limitant
La notion de réactif limitant est strictement liée aux proportions dictées par une équation chimique équilibrée. Nous avons, à plusieurs reprises, rappelé qu'une équation chimique équilibrée s'apparente à une recette de cuisine.
Recette de cuisine
| $2$ oeufs | $+$ | $3$ tasses de farine | $\ce{->}$ | $20$ cookies |
|---|---|---|---|---|
Veuillez bien noter que cette recette est incomplète: toutefois, on peut affirmer qu'ave $2$ oeufs et $3$ tasses de farine on peut faire $20$ cookies. D'autres ingrédients seront bien évidemment nécessaires (le beurre, par exemple).
Maintenant on change le nombre d'oeufs. Complétez le tableau:
| Nombre d'oeufs | Tasses de farine | Nombre de cookies | ||
|---|---|---|---|---|
| $4$ | $+$ | $..........................$ | $\ce{->}$ | $..........................$ |
Et maintenant, que se passe-t-il si on ne respecte pas les proportions: exemple, on a à disposition trop d'oeufs.
| Nombre d'oeufs | Tasses de farine | Nombre de cookies | Reste d' $.........$ | |||
|---|---|---|---|---|---|---|
| $3$ | $+$ | $3$ | $\ce{->}$ | $..........................$ | + | $..........................$ |
Equation chimique
Complétez le tableau
| $\ce{N2}$ | $+$ | $\ce{3 H2}$ | $\ce{->}$ | $\ce{2 NH3}$ | |
|---|---|---|---|---|---|
| proportions | |||||
| moles | $3$ |
Entourez le réactif limitant et déterminez les moles de $\ce{NH3}$ formées .
| $\ce{N2}$ | $+$ | $\ce{3 H2}$ | $\ce{->}$ | $\ce{2 NH3}$ | $+$ | Reste de $.........$ | |
|---|---|---|---|---|---|---|---|
| proportions | |||||||
| moles | $4$ | $9 $ | |||||
| moles | $4$ | $13 $ |
On remarque que les moles et donc les masses obtenues dépendent du réactif limitant.
Exercices Masse et Matière SERIE B
Quelles sont les particules présentes dans le bécher si on ajoute $0,38\,\mathrm{g}$ de $\ce{NaOH}$ à $0,645\,\mathrm{g}$ de $\ce{CoCl2}$ ?
Justifiez la réponse.
Quelle masse d’azoture de sodium $\ce{NaN3}$ faut-il pour produire un volume de $15\,\mathrm{L}$ aux CNTP ?
Dans une étude expérimentale en solution aqueuse, on a constaté que $0,48\,\mathrm{g}$ de titane ($III$) étaient suffisants pour transformer complètement $1,25·10^{-3}\,\mathrm{mol}$ de chlore ($VII$), sans avoir de résidu d'aucun des deux réactifs. Après avoir apporté à chaque équation ci-dessous les modifications nécessaires, trouvez laquelle illustre correctement la réaction entre le chlore ($VII$) et le titane ($III$). Expliquez votre choix avec du texte et des calculs.
$\ce{Cl^{7+} + Ti^{3+} -> Cl+ + Ti^{4+}}$
$\ce{Cl^{7+} + Ti^{3+} → Cl^{0} + Ti^{4+}}$
$\ce{Cl^{7+} + Ti^{3+} → Cl^{-} + Ti^{4+}}$
Afin d'obtenir du nitrure de lithium ($\ce{Li3N}$), on mélange $7\,\mathrm{g}$ de $\ce{Li}$ et $7\,\mathrm{g}$ de $\ce{N2}$. Quelle masse de $\ce{Li3N}$ va-t-on obtenir ? Ecrivez l'équation chimique équilibrée et répondez à la question.
Autrefois utilisé comme moyen d'éclairage, l'acétylène brûle selon la réaction de combustion complète équilibrée : $$\ce{2 C2H2 + 5 O2 -> 4 CO2 + 2 H2O}$$
Sur la base de cette équation équilibrée, complétez le modèle ci-dessous, en dessinant
| à gauche | à droite |
|---|---|
| les molécules de dioxygène nécessaires pour brûler toutes les molécules d'acétylène |
les molécules de $\ce{CO2}$ et $\ce{H2O}$ ainsi obtenues. |
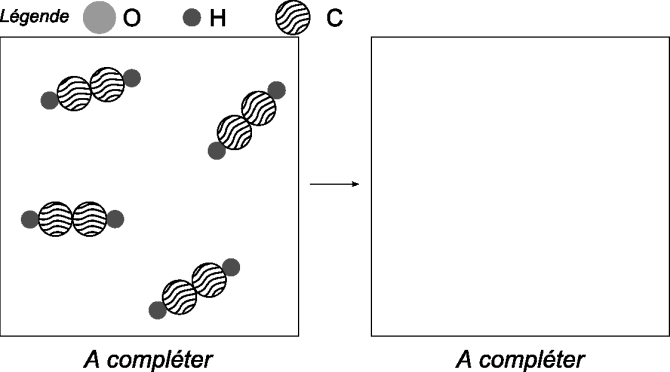
Dans le modèle suivant, un mélange contenant $2$ molécules de $\ce{C2H2}$ et $6$ d'$\ce{O2}$, est illustré. Complétez uniquement à droite, en dessinant les molécules obtenues et celles qui, éventuellement, n'ont pas réagi.